Sign of a permutation

0.00 When we defined the determinant of a matrix, we used the idea of the sign of a permutation. Permutations which can be written as an odd number of transpositions are given a minus sign; permutations which can be written as an even number of transpositions are given a plus sign. But why does this make sense? What if a permutation could be expressed in two ways, one involving an odd number of transpositions and one an even number? What would its sign be? This cannot occur: an odd permutation cannot be written as an even number of transpositions, and vice versa, but this is not obvious. The purpose of this video is to prove that the sign makes sense.

1.00 The proof I will present is inspired by a discussion on MathOverflow, in particular the answers of Ramras and Poonen, which explain a point of view originally due to Cartier.

1.30 Take an example: $\sigma=(1234)$ , the permutation which sends 1 to 2, 2 to 3, 3 to 4 and 4 back to 1. We draw a graph whose vertices are 1, 2, 3, 4 (more generally it will have $n$ vertices if we are permuting $n$ objects) and connect them with all possible edges. This is called the complete graph on $n$ vertices.

2.20 We will choose an orientation of this graph: that is, we draw an arrowhead on each edge to give a sense of direction. Apply $\sigma$ . The vertices move around and the arrows move around. We get a new orientation on the same graph; this is determined by the requirement that if we have an arrow from $i$ to $j$ then we get an arrow from $\sigma(i)$ to $\sigma(j)$ . We label each edge with a plus or a minus according to whether its direction has changed. For this example, three edges change, three do not.

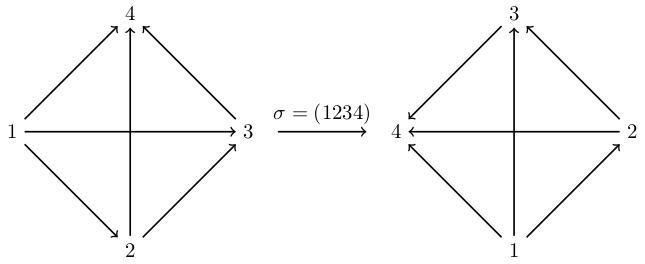
Applying a permutation to the orientation of the complete graph

Definition:

4.30 The sign of $\sigma$ is defined to be the product of the signs on the edges. In our example, this gives $+1\times+1\times+1\times-1\times-1\times-1=-1$ , so $\mathrm{sign}(\sigma)=-1$ .

5.00 It's not obvious that this is well-defined: maybe the sign depends on our original choice of orientation? It's also not obvious that this agrees with our original definition of the sign of a permutation (odd gives minus, even gives plus). We'll prove both of these.

Lemma:

The sign of $\sigma$ is well-defined.

Proof:

5.45 What happens if we flip one of the arrows in our original orientation? The corresponding arrow in the right-hand picture (after $\sigma$ ) also flips. If these two arrows are different, this gives us two edges whose signs change, which cancel in the product (leaving it unchanged). If the two arrows are the same then none of the signs on the edges change. Therefore $\mathrm{sign}(\sigma)$ doesn't depend on our choice of orientation (any two choices of orientation are related by a sequence of such flips).

Lemma:

This definition of $\mathrm{sign}(\sigma)$ agrees with our earlier one: odd permutations have negative sign; even permutations have positive sign.

Proof:

8.00 We split this up into two statements:

If $\sigma$ is a transposition then $\mathrm{sign}(\sigma)=-1$ .
$\mathrm{sign}(\sigma\circ\tau)=\mathrm{sign}(\sigma)\mathrm{sign}(\tau)$ .

Together, these facts tell us that the sign of an odd permutation is $-1$ and of an even permutation is $+1$ .

8.50 We first prove that the sign of a transposition is $-1$ . We focus on the part of the graph containing vertices $i$ and $j$ (which we are transposing). We choose an orientation such that the arrow between $i$ and $j$ points towards $j$ and all the other arrows involving $i$ or $j$ point away from $i$ or $j$ . When we transpose them, the only edge which changes direction is the one connecting $i$ and $j$ , so the overall sign is $-1$ .

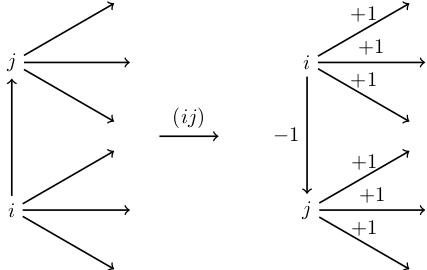
10.00 (Slightly different explanation to the video, better suited for writing.) To see that $\mathrm{sign}(\sigma)$ is multiplicative, think about each arrow individually. For each arrow there are four possibilities:

It switches under $\tau$ and also under $\sigma$ . Then it stays fixed under $\sigma\circ\tau$ . So this edge contributes a factor of $-1$ to both $\mathrm{sign}(\sigma)$ and $\mathrm{sign}(\tau)$ , and a factor of $+1$ to $\mathrm{sign}(\sigma\circ\tau)$
It switches under precisely one of $\sigma$ or $\tau$ and also under $\sigma\circ\tau$ . This edge contributes a $-1$ to one of $\mathrm{sign}(\sigma)$ or $\mathrm{sign}(\tau)$ and also a $-1$ to $\mathrm{sign}(\sigma\circ\tau)$ .
It doesn't switch under anything, which means it gives a factor of $1$ to all the signs.

In all cases, the contribution to $\mathrm{sign}(\sigma\circ\tau)$ equals the product of contributions to $\mathrm{sign}(\sigma)$ and $\mathrm{sign}(\tau)$ , so we see that $\mathrm{sign}$ is multiplicative.