Optional: Finding compact abelian subgroups

Compact abelian subgroups exist

This video is optional.

Proposition:

0.00 Any compact matrix group $G$ contains a compact abelian matrix group which is (a) path-connected and (b) nontrivial.

Remark:

In the next video, we'll see that any compact, path-connected abelian group is a torus, so together these results will show that $G$ contains a nontrivial torus.

Proof:

1.20 Let $\mathfrak{h}\subset\mathfrak{g}$ be a nontrivial abelian subalgebra, that is a subspace of $\mathfrak{g}$ on which the commutator bracket vanishes.

2.05 Note that there is always a nontrivial abelian subalgebra if $\mathfrak{g}$ is nontrivial, for example a line in $\mathfrak{g}$ is a nontrivial abelian subalgebra: suppose we look at the line spanned by $X\in\mathfrak{g}$ , then any two elements $\lambda_{1}X$ and $\lambda_{2}X$ of this line commute with one another.

3.05 We now make two claims:

$\exp(\mathfrak{h})=\{\exp(X)\ :\ X\in\mathfrak{h}\}$ is an abelian subgroup of $G$ .
while $\exp(\mathfrak{h})$ is not necessarily compact, its topological closure $\overline{\exp(\mathfrak{h})}$ is a compact abelian subgroup.

Together, these claims will prove the proposition (we just need to take the path-component of the identity in $\overline{\exp(\mathfrak{h})}$ ).

4.15 To prove claim 1, we observe that

$\exp(X_{1})\exp(X_{2})=\exp(X_{1}+X_{2})$ for all

$X_{1},X_{2}\in\mathfrak{h}$ because

$X_{1}$ and

$X_{2}$ commute. This implies that

$\exp(\mathfrak{h})$ is a subgroup of

$G$ , because if

$\exp(X_{1})\in\exp(\mathfrak{h})$ and

$\exp(X_{2})\in\exp(\mathfrak{h})$ then

$\exp(X_{1})\exp(X_{2})=\exp(X_{1}+X_{2})$ and

$X_{1}+X_{2}\in\mathfrak{h}$ because

$\mathfrak{h}$ is a subspace.

5.20 Moreover, $\exp(\mathfrak{h})$ is abelian, because:

$\exp(X_{1})\exp(X_{2})=\exp(X_{1}+X_{2})=\exp(X_{2}+X_{1})=\exp(X_{2})\exp(X_{% 1}).$

5.50 To prove claim 2, we showed earlier (as an exercise) that the topological closure of a subgroup is a subgroup, so we just need to show that $\overline{\exp(\mathfrak{h})}$ is compact and abelian. The fact that it's compact follows from the fact that it's closed (by construction) and contained in a compact set (the compact group $G$ ), and it's a general fact from point-set topology that a closed subset of a compact set is compact. (This is clear for us because "compact" means "closed and bounded", and a subset of a bounded set is bounded).

So the key thing to check is that $\overline{\exp(\mathfrak{h})}$ is abelian. This follows from the next lemma below.

Remark:

4.55 Note that it's not always true that exp of a Lie subalgebra gives a subgroup of $G$ .

Lemma:

6.40 If $H\subset G$ is an abelian subgroup then its topological closure $\bar{H}$ is abelian.

Proof:

$\bar{H}$ consists of limit points of sequences $h_{k}$ in $H$ which converge in $G$ . Suppose I have sequences $g_{k}\to g$ and $h_{k}\to h$ with $g_{k},h_{k}\in H$ , $g,h\in\bar{H}$ . Since $H$ is abelian, we have

$g_{k}h_{k}=h_{k}g_{k}\ \mbox{ for all }k.$ This implies that

$\lim g_{k}h_{k}=\lim h_{k}g_{k},$ so it's enough to show that

$\lim(g_{k}h_{k})=gh\mbox{ and }\lim(h_{k}g_{k})=hg.$

8.55 This follows from the fact that matrix multiplication is continuous. Let $m\colon GL(n,\mathbf{R})\times GL(n,\mathbf{R})\to GL(n,\mathbf{R})$ be matrix multiplication, i.e. $m(X,Y)=XY$ . This is continuous: it's actually a polynomial in the matrix entries. Therefore

$\lim m(g_{k},h_{k})=m(\lim g_{k},\lim h_{k})$ (you can "bring limits inside" continuous functions). This means exactly that

$g_{k}h_{k}\to gh,$ as required.

10.30 The proposition now follows by taking the path-component of the identity inside $\overline{\exp(\mathfrak{h})}$ .

Example

11.00 The following example should illustrate why I went to the bother of taking the topological closure and what it buys for us.

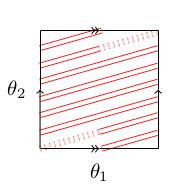
Let $G$ be the 2-dimensional torus $U(1)\times U(1)$ . We can draw it as a square with its opposite sides identified (the square lives in the $(\theta_{1},\theta_{2})$ -plane, and the side-identifications correspond to when $\theta_{1}$ or $\theta_{2}$ cross over a multiple of $2\pi$ and restart from zero.

Torus as a square with its opposite sides identified

11.50 On the square, a 1-parameter subgroup of $G$ will look like a bunch of straight line segments with the property that when one of the segments "leaves the square", another one re-enters the square at the opposite point (with the same slope).

12.05 Remember that a 1-parameter subgroup is precisely exp of a line in the Lie algebra. Pick a 1-parameter subgroup corresponding to a line of irrational slope. This will wrap around infinitely often in the group $G$ : in fact, it is dense in $G$ (comes arbitrarily close to any given point). The topological closure of this subgroup is then the whole of $G$ .

Dense line of irrational slope on a torus