Root spaces are 1-dimensional

Recap

If 𝔤 is the complexified Lie algebra of a compact semisimple group K then 𝔤=𝔥⊕⊕α∈R𝔤α where:

The figure below shows the root diagram of 𝔰𝔩(3,𝐂) . We've been gradually discovering that various nice features of this Lie algebra and its root diagram carry over to root diagrams in this more general context. These nice features include:

  • If α is a root then so is -α .

  • If X∈𝔤α and Y∈𝔤-α then X , Y and Hα=[X,Y] span a subalgebra Sα≅𝔰𝔩(2,𝐂) .

  • Partway through the proof of the previous point, we saw that [X,Y]=K(X,Y)α♯∈𝔥 , where α♯ is Killing-dual to α . This depends on X and Y only through their Killing pairing K(X,Y) . We also saw that if we pick X and Y suitably (so that K(X,Y)=2/K(α♯,α♯) ) then Hα=[X,Y]=2α♯K(α♯,α♯) satisfies the commutation relations [Hα,X]=2X,[Hα,Y]=-2Y,[X,Y]=Hα.

    • In this video, we will show that:

    Proposition:

    All the root spaces 𝔤α are 1-dimensional.

    Proof

    Fix a root α and consider the line through α . We will sum some of the root spaces along this line:

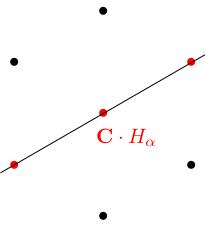
    Sum of root spaces along line through alpha

    The result is a subspace V=𝐂⋅Hα⊕⊕k∈𝐙∖{0}𝔤kα

    Lemma:

    V is preserved by the action of the subalgebra Sα . Moreover, it is irreducible as a representation of Sα .

    Remark:

    Irreducibility is the key thing, because this implies that the root spaces 𝔤kα are all 1-dimensional.

    Proof:

    We need to show that adX , adY and adHα preserve V . Let's just do adX (the others are similar/easier).

    • We have adXHα=[X,Hα]=-[Hα,X]=-2X∈𝔤α⊂V , so adX sends 𝐂⋅Hα to something in V .

    • We have adX:𝔤kα→𝔤(k+1)α because X∈𝔤α .

      • If k+1≠0 we have 𝔤(k+1)α⊂V and we're done.

      • If k+1=0 then 𝔤(k+1)α=𝔤0 , which is not contained in V . In fact, we have V∩𝔤0=𝐂⋅Hα , so we need to show that adXY is a multiple of Hα for any Y∈𝔤-α . But we saw that if X∈𝔤α and Y∈𝔤-α then [X,Y]=K(X,Y)α♯ , and α♯ is just a multiple of Hα , so adX(𝔤-α)=𝐂⋅Hα⊂V and we're done.

    How do we see that this representation is irreducible? Let's understand the weight space decomposition of V under the action of Sα . I claim that 𝔤kα is a weight space with weight 2k for the action of Hα .

    This is because if Z∈𝔤kα , we have adHαZ=kα(Hα)Z and, since H α = 2 ⁢ α ♯ / K ⁢ ( α ♯ , α ♯ ) , we have α ⁢ ( H α ) = 2 ⁢ α ⁢ ( α ♯ ) / K ⁢ ( α ♯ , α ♯ ) , but α ⁢ ( α ♯ ) = K ⁢ ( α ♯ , α ♯ ) , so ad H α ⁢ Z = 2 ⁢ k ⁢ Z and Z has weight 2 ⁢ k under the action of H α as required.

    So our weight diagram looks like this: ⋯ ⊕ 𝔤 - 2 ⁢ α ⊕ 𝔤 - α ⊕ 𝐂 ⋅ H α ⊕ 𝔤 α ⊕ 𝔤 2 ⁢ α ⊕ ⋯ in weights ⋯   - 4 , - 2 , 0 , 2 , 4 , ⋯ respectively. In particular, the weight space with weight zero is 𝐂 ⋅ H α , which is 1-dimensional. If we decompose V into irreducibles then these irreducibles all have even highest weight (there are only even weights) and in particular they will all have 1-dimensional weight space in weight zero. But there is only room for one such irreducible piece, so V must itself be irreducible.