6.01 Braids: Introduction
Below the video you will some pre-class questions and notes to accompany the video.
- Next video: Braids: Artin action.
- Index of all lectures.
Notes
Definitions
(0.00)
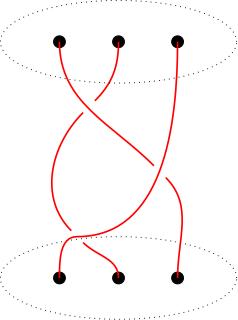
Fix a collection of \(n\) points \(z_1,\ldots,z_n\) in
\(\mathbf{C}\). An \(n\)-strand braid \(F\) is a collection
of \(n\) continuous maps \(F_1,\ldots,F_n\colon[0,1]\to\mathbf{C}\)
such that:
We can draw a picture of a braid as a collection of pairwise disjoint
paths \(\gamma_1,\ldots,\gamma_n\) in \(\mathbf{C}\times[0,1]\):
\[\gamma_k(t)=(F_k(t),t).\] In fact, since \([0,1]\) is compact and
the image of a compact set by a continuous map is compact, the images
of the paths \(F_k\) are contained in some compact set in the plane,
and we can always homotope everything (by a family of rescalings
depending on \(t\)) to assume that our braids are contained in
\(D\times[0,1]\), where \(D\) is the unit disc.
- \(F_i(t)\neq F_j(t)\) if \(i\neq j\)
- \(F_i(0)=z_i\), \(F_i(1)=z_{s(i)}\) for some permutation
\(s\colon\{1,\ldots,n\}\to\{1,\ldots,n\}\).
Equivalence of braids
(3.23) We say that two \(n\)-strand braids \(F\) and \(G\)
are equivalent if there is a collection of homotopies
\(H_k(s,t)\), \(k=1,\ldots,n\), such that \(\{H_k(s,t)\}_{k=1}^n\)
is a braid for each fixed value of \(s\) and such that
\[H_k(0,t)=F_k(t),\ H_k(1,t)=G_k(t),\]
Group law
(5.20) If \(F\) and \(G\) are two \(n\)-strand braids with
associated permutations \(\sigma\) and \(\tau\) respectively then
their product \(G\cdot F\) is the braid \[ (G\cdot F)_i(t)
=\begin{cases} F_i(2t)&\mbox{ if
}t\in[0,1/2]\\ G_{s(i)}(2t-1)&\mbox{ if }t\in[1/2,1]. \end{cases}
\]
Pictorially, we multiply braids by stacking them:
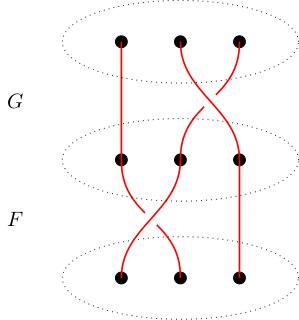
The set of equivalence classes of \(n\)-strand braids form a group \(B_n\)
under this stacking product.
This is an exercise.
Much of the proof of this theorem should look a little bit like the
proof that the fundamental group is a group. This is not a
coincidence: the \(n\)-strand braid group is the fundamental
group of a particular space, the unordered configuration space of
\(n\) points in the disc.
Configuration space
(8.20) Let \(OC_n\) be the subset of \(\mathbf{C}^n\) defined
by \[OC_n:=\{(x_1,\ldots,x_n)\in \mathbf{C}^n\ :\ x_i\neq x_j\mbox{
for }i\neq h\}.\] We call a point \((x_1,\ldots,x_n)\in OC_n\) an
ordered configuration of points in the disc and \(OC_n\) is
called the ordered configuration space of \(n\) points in the
plane. There is an action of the permutation group \(S_n\) on
\(OC_n\); a permutation \(s\) acts as
\[(x_1,\ldots,x_n)s=(x_{s(1)},\ldots,x_{s(n)}).\] The quotient
\(UC_n:=OC_n/S_n\) is called the space is called the unordered
configuration space of \(n\) points in the plane.
The fundamental group \(\pi_1(UC_n,[z_1,\ldots,z_n])\) is isomorphic
to the \(n\)-strand braid group.
This should be clear from the definition of a braid: a braid is a
collection of paths \(F_1(t),\ldots, F_n(t)\) with \(F_i(t)\neq
F_j(t)\) if \(i\neq j\) and such that \(F_i(0)=z_i\),
\(F_i(1)=z_{s(i)}\). Such a collection of paths defines a loop: \[
[F_1(t),\ldots,F_n(t)]\] in the unordered configuration space based
at \([z_1,\ldots,z_n]\) and conversely. A homotopy of braids gives a
homotopy of loops in the unordered configuration space (again, just
by definition). Stacking braids corresponds to concatenating loops.
Presentation of the braid group
(11.38) We will assume that the points \(z_i\) are equally
spaced along a line. For each \(i=1,2,\ldots,n-1\) there is an
elementary braid:



The braid group \(B_n\) is generated by the elementary braids
subject to the following relations:
\begin{gather*}
\sigma_i\sigma_j=\sigma_j\sigma_i\mbox{ if }|i-j|\geq 1\\
\sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1}.
\end{gather*}
Proof not included! It is an exercise to check that the braid
relations hold. Later, I will give \(\epsilon\) more explanation for
how one would go about checking that these relations suffice.
Pre-class questions
- Why do braids form a group under stacking?
Navigation
- Next video: Braids: Artin action.
- Index of all lectures.