8.03 Normal covering spaces

Below the video you will find accompanying notes and some pre-class questions.

Notes

Example

(0.25) Consider the covering space \(p_n\colon S^1\to S^1\), \(p_n(z)=z^n\). What is the deck group of this covering space? Deck transformations are covering isomorphisms \(F\colon(S^1,p_n)\to (S^1,p_n)\), satisfying \(p_n\circ F=p_n\). In other words, \[(F(z))^n=z^n\] so \(F(z)=\mu z\) for some \(\mu\) with \(\mu^n=1\). The formula \(F(z)=\mu z\) defines a deck transformation for each \(n\)th root of unity, and any deck transformation must have this form. This tells us that the deck group is \[Deck(S^1,p_n)=\mathbf{Z}/n.\]

(2.15) If we take \(\pi_1(S^1,1)=\mathbf{Z}\) and push it forward along \(p_n\) then we get the subgroup \[(p_n)_*\pi_1(S^1,1)=n\mathbf{Z}\subset\pi_1(S^1,1)=\mathbf{Z}.\] Note that, in this example, \[Deck(S^1,p_n)\cong\mathbf{Z}/(n\mathbf{Z})=\pi_1(X,x)/p_*\pi_1(Y,y)\] where \(p\colon Y\to X\) is the covering space.

(3.36) Consider the covering space \(p\colon\mathbf{R}\to S^1\), \(p(x)=e^{2\pi ix}\). What is the deck group? It consists of maps \(F\colon\mathbf{R}\to\mathbf{R}\) such that \(e^{2\pi iF(x)}=e^{2\pi ix}\), which implies \(F(x)=x+n\). The deck group is therefore \(Deck(\mathbf{R},p)=\mathbf{Z}\). The pushforward \(p_*\pi_1(\mathbf{R})\) is trivial as \(\mathbf{R}\) is simply-connected, so the quotient \(\pi_1(S^1)/p_*\pi_1(\mathbf{R})\) is isomorphic to \(\mathbf{Z}\), which is the deck group.

Normal subgroups

(5.40) Is this a general phenomenon? No: the subgroup \(p_*\pi_1(Y,y)\subset\pi_1(X,x)\) might not be a normal subgroup, in which case the quotient \(\pi_1(X,x)/p_*\pi_1(Y,y)\) doesn't even make sense. However, in the case where \(p_*\pi_1(Y,y)\) is a normal subgroup of \(\pi_1(X,x)\), it will turn out to be true that \(Deck(Y,p)=\pi_1(X,x)/p_*\pi_1(Y,y)\). We single out these covers with a definition:

(6.56) We say that \(p\colon Y\to X\) is a normal (or regular, or Galois) cover if \(p_*\pi_1(Y,y)\) is a normal subgroup of \(\pi_1(X,p(y))\).

Normal covering spaces are maximally symmetric, as we will see from the following lemma.

(7.34) A path-connected covering space \(p\colon Y\to X\) is normal if and only if \(Deck(Y,p)\) acts transitively on \(p^{-1}(x)\) for some \(x\in X\).

(8.45) Note that \(Deck(Y,p)\) always acts on \(p^{-1}(x)\): if \(F\in Deck(Y,p)\) and \(y\in p^{-1}(x)\) then \(p(F(y))=p(y)=x\), so \(F(y)\in p^{-1}(x)\).

(9.56) Moreover, \(F\in Deck(Y,p)\) is determined uniquely by its value on a particular point \(y\in p^{-1}(x)\): indeed, any covering transformation is determined uniquely by its value at a point. Therefore, if the action of \(Deck(Y,p)\) is transitive on \(p^{-1}(x)\), then \(Deck(Y,p)\) is as big as it could possibly be: if it were any bigger, two of its elements would necessarily agree at some point \(y\in p^{-1}(x)\), and hence would be equal.

(12.29) In our earlier examples, the deck group acts transitively. For \(p_n\colon S^1\to S^1\), the \(n\)th roots of unity act transitively by rotation on \(p_n^{-1}(1)\), which it itself the set of \(n\)th roots of unity. For \(p\colon\mathbf{R}\to S^1\), the group \(\mathbf{Z}\) acts transitively by translation on \(p^{-1}(1)=\mathbf{Z}\).

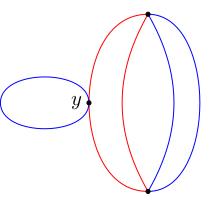
(14.03) Below is a covering space of the figure 8 which is not normal.

Let \(x\) be the cross-point of the figure 8. It has three pre-images, but only one of these (say \(y\)) is the endpoint of a blue loop. Since deck transformations are symmetries of the covering space, they must preserve the unique blue loop, and hence fix this point \(y\). If a deck transformation fixes a point then it is equal to the identity, by uniqueness. Therefore the deck group in this case is trivial.

Proof of lemma

(16.57) Assume that \(Deck(Y,p)\) acts transitively on \(p^{-1}(x)\). Pick \(\beta\in\pi_1(X,x)\). We want to show that \[\beta p_*\pi_1(Y,y)\beta^{-1}=p_*\pi_1(Y,y).\] We know from an exercise in an earlier class that \[\beta p_*\pi_1(Y,y)\beta^{-1}=p_*\pi_1(Y,\sigma_\beta(y)),\] where \(\sigma_\beta\colon p^{-1}(x)\to p^{-1}(x)\) is the monodromy around \(\beta\). Therefore it suffices to prove that \(p_*\pi_1(Y,y)=p_*\pi_1(Y,\sigma_\beta(y))\).

(19.34) By assumption, \(Deck(Y,p)\) acts transitively, so there exists a deck transformation \(F\colon Y\to Y\) such that \(F(y)=\sigma_\beta(y)\) and deck transformations are homeomorphisms, so \[(F_*\colon\pi_1(Y,y)\to\pi_1(Y,\sigma_\beta(y))\] is an isomorphism. We also know that \(p\circ F=p\), so \(p_*\circ F_*=p_*\). Putting all this together gives: \begin{align*} \beta p_*\pi_1(Y,y)\beta^{-1}&= p_*\pi_1(Y,\sigma_\beta(y))\\ &=p_*(F_*(\pi_1(Y,y)))\\ &=p_*\pi_1(Y,y). \end{align*} Since this holds for all \(\beta\in\pi_1(X,x)\), this shows that \(p_*\pi_1(Y,y)\subset\pi_1(X,x)\) is normal.

(21.50) Conversely, suppose that \(p_*\pi_1(Y,y)\) is a normal subgroup. Let \(y'\) be another point in \(p^{-1}(x)\) and let \(\tilde{\beta}\) be a path in \(Y\) from \(y\) to \(y'\). Then \(y'=\sigma_\beta(y)\) and \[p_*\pi_1(Y,y')=\beta p_*\pi_1(Y,y)\beta^{-1}.\] Since \(p_*\pi_1(Y,y)\) is normal, we get \(p_*\pi_1(Y,y')=p_*\pi_1(Y,y)\), so the existence theorem for covering isomorphisms implies that there exists a covering transformation \(F\colon Y\to Y\) such that \(F(y)=y'\). Therefore \(Deck(Y,p)\) acts transitively on \(p^{-1}(x)\).

Pre-class questions

  1. Consider the non-normal covering space example. What is the subgroup \(p_*\pi_1(Y,y)\subset\pi_1(X,x)\)? Can you see it is not normal without appealing to the lemma we used?

Navigation