1.08 Brouwer's fixed point theorem

Below the video you will find accompanying notes and some pre-class questions.

• Previous video: 1.07 Induced maps.
• Next video: 1.09 Homotopy equivalence.
• Index of all lectures.

Notes

Brouwer's fixed point theorem

(1.40) Assume, for a contradiction, that \(F(x)\neq x\) for all \(x\in D^2\). Then we can define a map \(G\colon D^2\to\partial D^2\) (where \(\partial D^2\) denotes the boundary circle) as follows: consider the ray starting at \(F(x)\), passing through \(x\) and let \(G(x)\) to be the unique point of intersection of this ray with \(\partial D^2\).

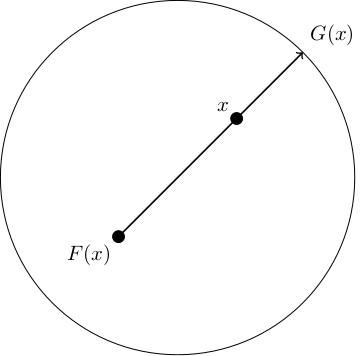
(3.45) If there were a fixed point, we would not know which ray to draw (as \(F(x)=x\)), so this map is only well-defined because we have assumed there are no fixed points.

(3.58) We claim that:

1. \(G\) is continuous; this is intuitively clear, but requires proof (below).
2. \(G(x)=x\) if \(x\in\partial D^2\); this is clear, because if \(x\in\partial D^2\), no matter where \(F(x)\) is, the ray from \(F(x)\) to \(x\) intersects the boundary at \(x\), so \(G(x)=x\).

(5.25) Given these two claims, we get a contradiction as follows. Let \(i\colon\partial D^2\to D^2\) be the inclusion map of the boundary; the composition \(G\circ i\) equals the identity map on \(\partial D^2\) by claim 2. This implies \[id=G_*\circ i_*\colon\pi_1(\partial D^2)\to\pi_1(\partial D^2).\] We have \(\pi_1(\partial D^2)=\mathbf{Z}\), and this is saying that the identity map on the integers factors through the map \(i_*\colon\pi_1(\partial D^2)\to\pi_1(D^2)=0\):

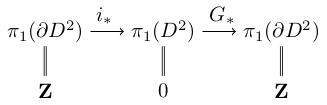
(9.20) It remains to prove claim 1 (that \(G\) is continuous). We can write \(G\) as a composition \(H\circ j\) where:

• \(j\colon D^2\to D^2\times D^2\setminus\{(x,x)\ :\ x\in D^2\}\) is the map \(j(x)=(x,F(x))\).
• (11.30) \(H\colon D^2\times D^2\setminus\{(x,x)\ :\ x\in D^2\}\) is the map defined as follows. Given two distinct points \(x\neq y\) in \(D^2\), let \(H(x,y)\) denote the point where the ray from \(y\) through \(x\) intersects \(\partial D^2\).

(13.25) We can write \(H\) explicitly in coordinates. The ray from \(y\) through \(x\) is given in parametric form by \(y+t(x-y)\). The condition that the ray meets the boundary of the disc is \[|y+t(x-y)|^2=1,\] which is a quadratic equation in \(t\): \[t^2|x-y|^2+2t(x-y)\cdot y+|y|^2-1=0.\] (Note that the leading term is never zero since \(x\neq y\)). This has solution \[t_\pm=\frac{-2(x-y)\cdot y\pm\sqrt{4((x-y)\cdot y)^2-4|x-y|^2(|y|^2-1)}}{2|x-y|^2}\] We are only interested in solutions with \(t\geq 0\) as the ray only points in one direction. Therefore the point \(H(x,y)\) is \(y+t_+(x-y)\), which is now expressed purely in terms of rational functions and surds, all of which are continuous.

Pre-class questions

1. Brouwer's fixed point theorem tells us that continuous maps between 2-discs have fixed points. Is the same true for maps between 2-dimensional annuli? (An annulus is \(S^1\times[0,1]\)).
2. Brouwer's fixed point theorem also holds for maps \(F\colon D^n\to D^n\) where \(D^n\) is the \(n\)-dimensional disc; can the proof above be adapted to cover this case, or are new ideas required?

Navigation

• Previous video: 1.07 Induced maps.
• Next video: 1.09 Homotopy equivalence.
• Index of all lectures.