2.02 Bases, metric and product topologies

Below the video you will find accompanying notes and some pre-class questions.

Previous video: Topological spaces, continuous maps.
Next video: Subspace topology.
Index of all lectures.

Notes

(0.00) In the last section, we defined topological spaces. In this section, I will tell you how you might specify a topology on a set. The idea comes from the theory of metric spaces.

Bases and the metric topology

(0.25) Given a metric space \((X,d)\), how do I define a topology on \(X\)? Let \(\mathcal{B}=\{B_r(x)\ :\ x\in X,\ r\geq 0\}\) be the set of all (open) metric balls in \(X\). Let \(T=\{\mbox{arbitrary unions of balls in }\mathcal{B}\}\).

(1.53) We will see in a moment that \(T\) is a topology \(X\); in general, this is a good way to specify a topology: you specify a set \(\mathbf{B}\) of sets you want to be open and take as your topology the set of arbitrary unions of sets in \(\mathcal{B}\). It doesn't always work (we will see below some conditions on \(\mathcal{B}\) which ensure that it does work). When this construction yields a topology \(T\), we say that \(\mathcal{B}\) is a base for \(T\).

(2.50) \(T\) is a topology on \(X\), called the metric topology.

The empty set is in \(T\) because it is the empty union of sets from \(\mathcal{B}\).

\(X\) is in \(T\) because for any \(x\in X\) the ball \(B_1(x)\) contains \(x\), so \(X\) equals the union \(\bigcup_{x\in X}B_1(x)\), which is in \(T\) by definition (it is a union of sets from \(\mathcal{B}\)).

Unions of sets in \(T\) are unions of unions of sets in \(B\), so in particular they are unions of sets in \(B\) and therefore in \(T\). So \(T\) is closed under taking union.

(4.06) All that remains is to show that if \(U,V\in T\) then \(U\cap V\in T\).

Given a point \(x\in U\cap V\), we need to show that \(x\) is contained in a ball \(B_{\epsilon_x}(x)\in\mathcal{B}\) such that \(B_{\epsilon_x}(x)\subset U\cap V\): then we have \(U\cap V=\bigcup_{x\in U\cap V}B_{\epsilon_x}(x)\) which is in \(T\) by definition. Since \(U\in T\) and \(x\in U\) we know that there is some ball \(B_s(u)\in\mathcal{B}\) with \(x\in B_s(u)\subset U\). Similarly, there is a ball \(B_t(v)\in\mathcal{B}\) with \(x\in B_t(v)\subset V\).

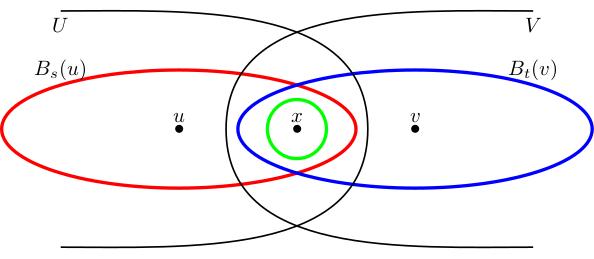
(6.22) We need to check that there is some radius \(\epsilon_x\) such that \(B_{\epsilon_x}(x)\subset B_s(u)\cap B_t(v)\).

Let \(\epsilon_1=s-d(u,x)\). I claim that \(B_{\epsilon_1}(x)\subset B_s(u)\): if \(w\in B_{\epsilon_1}(x)\) then \(d(w,u)\leq d(w,x)+d(x,u)<\epsilon_1+d(u,x)=s\), so \(w\in B_s(u)\).

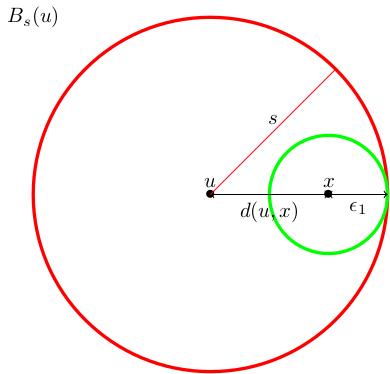
(8.55) Similarly, if \(\epsilon_2=t-d(x,v)\) then \(B_{\epsilon_2}(x)\subset B_t(v)\). Set \(\epsilon_x=\min(\epsilon_1,\epsilon_2)\); then \(B_{\epsilon_x}(x)\subset B_s(u)\cap B_t(v)\) as required.

The moral of the proof is this:

(9.47) Let \(X\) be a set, let \(\mathcal{B}\) be a collection of subsets of \(X\). Let \(T\) be the set of subsets of \(X\) which are arbitrary unions of sets in \(\mathcal{B}\). Then \(T\) is a topology if:

for all \(x\in X\) there exists \(b\in\mathcal{B}\) such that \(x\in b\) (this will imply \(X\in T\));
for all \(U,V\in\mathcal{B}\) and \(x\in U\cap V\) there exists \(b\in\mathcal{B}\) such that \(x\in b\subset U\cap V\) (this will imply that \(T\) is closed under taking finite intersections).

If these conditions hold, we say that \(\mathcal{B}\) is a base for the topology \(T\).

Base for the product topology

(13.32) If \((X,S)\) and \((Y,T)\) are topological spaces, we can put a topology on their product \(X\times Y\) by specifying a base: we let \(\mathcal{B}\) be the set \(\{U\times V\ :\ U\in S,\ V\in T\}\).

(14.43) In the figure we take \(X=Y=[0,1]\) with its metric topology and we can see a set which is in the topology \(T\) but not in the base \(\mathcal{B}\) (it is a union of open rectangles but not an open rectangle).

(15.39) If \((X,S)\) and \((Y,T)\) are topological spaces, \(\mathcal{B}=\{U\times V\ :\ U\in S,\ V\in T\}\) is a base (so the definition above makes sense).

We need to check two things:

(16.10) For all \((x,y)\in X\times Y\) there exist \(U\in S\) such that \(x\in U\) and \(V\in T\) such that \(y\in V\), so \((x,y)\in U\times V\in\mathcal{B}\).
(17.08) Given \(U_1\times V_1\) and \(U_2\times V_2\), the intersection is \((U_1\times V_1)\cap (U_2\times V_2)=(U_1\cap U_2)\times (V_1\cap V_2)\).

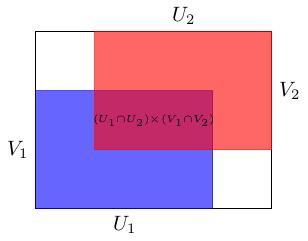
Since \(U_1\cap U_2\in S\) and \(V_1\cap V_2\in T\), \((U_1\cap U_2)\times (V_1\cap V_2)\in\mathcal{B}\).

This implies that \(\mathcal{B}\) is a base.

Pre-class questions

In this video, instead of checking that all finite intersections of open sets are open, we checked that intersections of two open sets are open. Why is this sufficient?
Let \(X\) be a set. Can you give a base for the discrete topology on \(X\)? What is the smallest base you could give?

Navigation

Previous video: Topological spaces, continuous maps.
Next video: Subspace topology.
Index of all lectures.