5.04 Proof of Van Kampen's theorem

Below the video you will find accompanying notes and some pre-class questions.

Notes

This proof is nonexaminable. I don't want you to memorise it. It's a long and tricky proof, but the payoff is that Van Kampen's theorem is the most powerful theorem in this module and once you have understood why it's true (by following the proof) you can be confident about using it.

Strategy of proof

(0.00) Suppose we have decomposed \(X\) as a union \(U\cup V\) where \(U\cap V\) is path-connected. Pick a point \(x\in U\cap V\). We want to show that \(\pi_1(X,x)=\pi_1(U,x)\star_{\pi_1(U\cap V,x)}\pi_1(V,x)\).

(1.06) Equivalently, we know that the amalgamated product is a quotient of \(\pi_1(U,x)\star\pi_1(V,x)\) be a normal subgroup \(Amal\), normally generated by the amalgamated relations, that is by words of the form \(i_*(c)j_*(c)^{-1}\), where \(i\colon U\cap V\to U\) and \(j\colon U\cap V\to V\) are the inclusion maps.

(3.05) We should therefore try to find a surjective homomorphism \(\phi\colon\pi_1(U,x)\star\pi_1(V,x)\to \pi_1(X,x)\) whose kernel is the subgroup \(Amal\). By the first isomorphism theorem, this will imply that \(\pi_1(X,x)=(\pi_1(U,x)\star\pi_1(V,x))/Amal\).

(4.20) The map \(\phi\) is easy to define: an element of \(\pi_1(U,x)\star\pi_1(V,x)\) is a word whose letters are (homotopy classes of) loops in \(U\) based at \(x\) or loops in \(V\) based at \(x\). Given such a word, \(u_1v_1\cdots u_nv_n\) (where \(u_i\in\pi_1(U,x)\) and \(v_i\in\pi_1(V,x)\) we get an element \[\phi(u_1v_1\cdots u_nv_n)=a_*(u_1)b_*(v_1)\cdots a_*(u_n)b_*(v_n),\] where \(a\colon U\to X\) and \(b\colon V\to X\) are the inclusion maps.

(6.38) This gives a map \(\phi\colon\pi_1(U,x)\star\pi_1(V,x)\to\pi_1(X,x)\) which is clearly a homomorphism by the way it is defined. We need to show that

  1. \(\phi\) is surjective,
  2. \(\ker\phi=Amal\).

Surjectivity of \(\phi\)

(7.56) Given any loop based at \(x\), we want to write it (up to homotopy) as a concatenation of loops which are contained entirely in either \(U\) or in \(V\). The idea is to ``pinch off subloops''.

(9.23) Rigorously, we proceed as follows. Pick a loop \(\gamma\colon[0,1]\to X\) based at \(x\). Since the interval \([0,1]\) is compact, and since \(\gamma\) is continuous, the interval can be subdivided into finitely many segments \([t_i,t_{i+1}]\) such that the image of \(\gamma_i:=\gamma|_{[t_i,t_{i+1}]}\) is contained entirely in \(U\) or entirely in \(V\).

(12.45) Each path \(\gamma_i\) can be capped off to make it into a loop. More precisely, pick a path \(\beta_i\subset U\cap V\) from \(x\) to \(\gamma(t_i)\) and note that if \(\gamma_i\) is contained in \(U\) (respectively \(V\)) then \(\beta_{i+1}^{-1}\cdot\gamma_i\cdot\beta_i\) is a loop contained in \(U\) (respectively \(V\)).

(16.12) Now the concatenation \[(\beta_{n}^{-1}\gamma_{n-1}\beta_{n-1})\cdots(\beta_{n-1}^{-1}\gamma_{n-2}\beta_{n-3})\cdots(\beta_1^{-1}\gamma_0\beta_0)\] is homotopic to \[\beta_{n}^{-1}\gamma_{n-1}\gamma_{n-2}\cdots\gamma_0\beta_0\] just by cancelling all the \(\beta^{-1}\beta\) terms. Since \(\gamma\) starts and ends at \(x\), we may as well assume that \(\beta_0=\beta_n\) is the constant path, so this concatenation is homotopic to \(\gamma\). Therefore, up to homotopy, we see that \([\gamma]=\phi([\gamma_{n-1}]\cdots[\gamma_0])\), with each \([\gamma_i]\) in either \(\pi_1(U,x)\) or \(\pi_1(V,x)\), so we have found a \(\phi\)-preimage for \([\gamma]\) and proved that \(\phi\) is surjective.

\(\ker\phi=Amal\)

(18.17) \(\ker\phi\) comprises words \([u_1][v_1]\cdots [u_n][v_n]\) of homotopy classes of loops \(u_i\) in \(U\) and \(v_i\) in \(V\) such that \(a(u_1)b(v_1)\cdots a(u_n)b(v_n)\) is nullhomotopic (recall that \(a\colon U\to X\) and \(b\colon V\to X\) are the inclusion maps). Pick a nullhomotopy \(H\) from this concatenation to the constant loop at \(x\).

(20.42) \(H\) is a map \([0,1]\times[0,1]\to X\) where:

(21.45) We would now like to subdivide the square into smaller squares such that \(H\) restricted to those smaller squares is either a homotopy in \(U\) or in \(V\). This is possible because the square is compact and \(H\) is continuous.

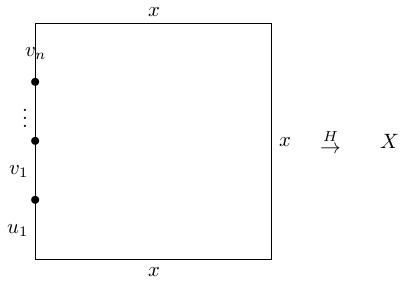
(23.32) We can assume that this grid of subsquares is a refinement of the \(2n\)-by-\(2n\) grid which gives the subdivision of the left-hand edge into subpaths \(u_i,v_i\).

(24.09) For simplicity, we will restrict to a 2-by-2 grid (this makes our notation/lives easier without losing any of the ideas of the proof). In particular, we will assume that \(n=1\) and write \(u_1=u\), \(v_1=v\). We therefore have the picture below: the restriction of \(H\) to each outside edge is indicated and each subsquare is mapping to either \(U\) or to \(V\) via \(H\).

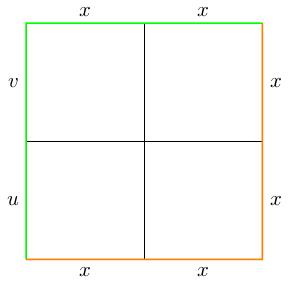
(25.00) Consider the green path in the figure above which runs up the left-hand edge and across the top edge of the square. The restriction of \(H\) to this path gives the loop \(uvxx\) (where \(x\) denotes the constant path at \(x\)). This loop is homotopic to the concatenation \(uv\) we began with, which is in the kernel of \(\phi\).

(25.45) Analogously, the orange path (running along the bottom edge and up the right-hand edge) gives the constant path at \(x\). We will think of this as the concatenation \(xxxx\). We will write down a sequence of paths \begin{align*} \lambda^1_1\lambda^1_2\lambda^1_3\lambda^1_4&=uvxx\\ \lambda^2_1\lambda^2_2\lambda^2_3\lambda^2_4&\\ \vdots&\\ \lambda^n_1\lambda^n_2\lambda^n_3\lambda^n_4&=xxxx. \end{align*}

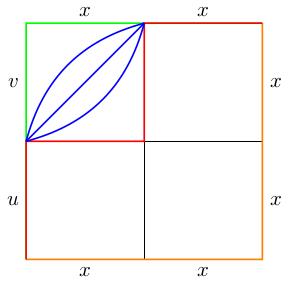
(26.44) These paths are obtained by restricting \(H\) to a sequence of stair-like paths in our grid (each step involves switching two segments running up and along the top of a subsquare with the corresponding segments running along the bottom and up the side of the same subsquare; the first of these is the red path below, which is homotopic to the green path via the blue homotopy, which happens only in one square).

(27.38) In a dream-version of this proof, we would say that these \(\lambda\)s are loops (they're not) and each subsequent path is obtained from the one before it by a based homotopy which happens entirely in \(U\) or entirely in \(V\). Therefore we only need to use relations from \(\pi_1(U,x)\) or \(\pi_1(V,x)\); sometimes, when \(\lambda_i^j\) has its image contained entirely in \(U\cap V\), we may need to switch between considering it inside \(U\) or inside \(V\) before we use these relations, and that amounts to using the amalgamated relations. This implies that \(uv\) is in the normal subgroup generated by the amalgamated relations.

(31.21) To get around the fact that the \(\lambda\)s might not be loops, we first modify our homotopy to ensure that each \(\lambda_i^j\) is a loop. In other words, we need to find a new homotopy \(H\) such that \(H(s,t)=x\) for all nodes \((s,t)\) of our grid (then the restrictions of \(H\) to edges will be loops based at \(X\)).

(32.37) Let us modify our homotopy to make the central vertex (call it \(p\)) map to \(x\). Pick a path \(\delta\) from \(x\) to \(H(p)\). Let \(S=[0,1]^2\) be the square and consider a disc \(D\subset S\) of small radius \(\epsilon>0\) around \(p\). Consider the quotient map \(q\colon S\to S/D\). the quotient \(S/D\) is homeomorphic to \(S\) and we can assume that the disc \(D\) is crushed to the point \(p\). The composition \(H':=H\circ q\colon S\to X\) now satisfies \((H'|_D=\mbox{const}\), \(H'(D)=H(p)\). Along the boundary \(\partial S\) the maps \(H\) and \(H'\) agree, so \(H'\) is as good a homotopy as \(H\) for the purposes of our proof.

(35.15) We now modify \(H'\) on the subset \(D\) to get a new homotopy \(H''\) which agrees with \(H\) on \(\partial S\) (so can again be used for the proof). We will ensure that \(H''(p)=x\) as required. On \(S\setminus D\), we define \(H''|_{S\setminus D}=H'|_{S\setminus D}\). On \(D\), we use polar coordinates \(re^{i\theta}\) and define \(H''(re^{i\theta})=\delta(r/\epsilon)\). Note that since \(D\) has radius \(\epsilon\), \(H''(\partial D)=\delta(1)=H(p)=H'(\partial D)\) (so \(H''\) is continuous). We also have \(H''(0)=\delta(0)=x\) and \(0\) here means the centre of \(D\), i.e. the point \(p\). So \(H''(p)=x\) as required.

(37.20) We need to be slightly careful that \(H''\) still sends the subsquares to either \(U\) or to \(V\). This holds as long as \(\delta\) is contained entirely inside \(U\) or entirely inside \(V\) or entirely inside \(U\cap V\) (depending on where the neighbouring squares map).

(38.46) This completes the proof. The last few minutes of the video recaps the proof.

Pre-class questions

  1. Justify the claim that \(\phi\) is a homomorphism.
  2. Within the proof that \(\phi\) is surjective, where did we use the fact that \(U\cap V\) is path-connected?
  3. Do we need to assume that \(U\) and \(V\) are path-connected too?

Navigation

Comments, corrections and contributions are very welcome; please drop me an email at j.d.evans at lancaster.ac.uk if you have something to share.

CC-BY-SA 4.0 Jonny Evans.