Cyclic quotient singularities

[2018-06-02 Sat]

I have been reading the paper "Flipping surfaces" by Hacking, Tevelev and Urzúa, which is a detailed study of a certain class of 3-fold flips. There is some background material about cyclic quotient surface singularities which I keep having to figure out from first principles whenever I return to this stuff and it would be helpful to have it written down somewhere. To that end, here is the first in a series of posts about this, covering the toric model for cyclic quotient singularities and the minimal resolution.

Toric picture of cyclic quotient singularities

Given coprime positive integers \(P,Q\), the cyclic quotient singularity of type \(\frac{1}{P}(1,Q)\) is defined to be the quotient \(\mathbf{C}^2/\Gamma\) where \(\Gamma\) is the action of the group of \(P^{th}\) roots of unity on \(\mathbf{C}^2\) given by \(\mu\cdot(x,y)=(\mu x,\mu^Q y)\).

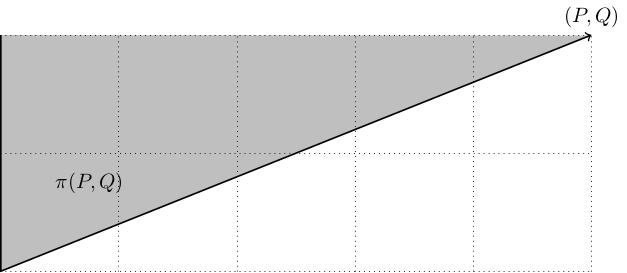
The singularity \(\mathbf{C}^2/\Gamma\) admits a Hamiltonian torus action generated by a moment map \(\mu\colon\mathbf{C}^2/\Gamma\to\mathbf{R}^2\) whose image is the wedge \[\pi(P,Q):=\{(x,y)\in\mathbf{R}^2\ :\ x\geq 0,\ Py\geq Qx\}.\]

The Hamiltonian functions \(H_1(x,y):=\frac{1}{2}|x|^2\) and \(H_2(x,y):=\frac{1}{2}|y|^2\) on \(\mathbf{C}^2/\Gamma_{P,Q}\) Poisson-commute and generate an \(\mathbf{R}^2\)-action whose period lattice is the set of points \[(\phi_1,\phi_2)=\left(2\pi\left(\frac{k}{P}+\ell\right), 2\pi\left(\frac{kQ}{P}+m\right)\right),\quad k,\ell,m\in\mathbf{Z}.\] (The period lattice for an \(\mathbf{R}^n\)-action is the set of points in \(\mathbf{R}^n\) which act as the identity.) The Hamiltonians \(\frac{1}{P}(H_1+QH_2)\) and \(H_2\) therefore give us the standard period lattice \(2\pi\mathbf{Z}\oplus 2\pi\mathbf{Z}\), therefore define an effective Hamiltonian torus action. The image of \(\mathbf{C}^2/\Gamma_{P,Q}\) under \(\mu=\left(H_2,\frac{1}{P}(H_1+QH_2)\right)\) is precisely the polygon \(\pi(P,Q)\).

Minimal resolution

The minimal resolution \(\pi\colon\tilde{X}\to X\) of a cyclic quotient singularity \(X\) of type \(\frac{1}{P}(1,Q)\) has the following exceptional locus: it is a Hirzebruch-Jung chain of embedded spheres \(C_1,\ldots,C_r\):

with self-intersections \(C_i^2=-b_i\), where \[\frac{P}{Q}=[b_1,\ldots,b_r]:=b_1-\frac{1}{b_2-\frac{1}{\cdots-\frac{1}{b_r}}}.\] This is also toric; the moment polygon is obtained from \(\pi(P,Q)\) by iteratively truncating the non-Delzant vertices (i.e. the vertices where the primitive integer vectors pointing along the outgoing edges do not form a basis for \(\mathbf{Z}^2\)) in much the way that blowing-up a smooth toric fixed point corresponds to truncating a Delzant vertex. The polygon \(\tilde{\pi}(P,Q)\) is therefore a subset of \(\pi(P,Q)\); below we see the minimal resolution for \(\frac{1}{5}(1,2)\) (with \(b_1=3\), \(b_2=2\) and \(\frac{P}{Q}=\frac{5}{2}=3-\frac{1}{2}\).

From this toric picture we can easily verify that the self-intersections of the exceptional curves in the minimal resolution are the coefficients of the continued fraction of \(P/Q\):

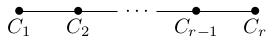
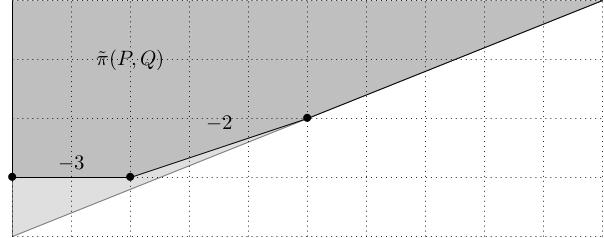
The first truncation should be made horizontally: this is the obvious way to ensure that the left-most vertex is Delzant.
The new right-hand vertex now has outgoing edge vectors \((-1,0)\) and \((P,Q)\); if we write \(P=b_1Q-R_1\) for some \(0\leq R_1\leq Q-1\) then the matrix \(\left(\begin{array}{cc}0&1\\ -1&b_1\end{array}\right)\) applied to these edge vectors sends them to \((0,1)\) and \((Q,R_1)\), so the new right-hand vertex corresponds to a cyclic quotient singularity of type \(\frac{1}{Q}(1,R_1)\). If \(R_1=0\) then this vertex is smooth, so we stop truncating.
Otherwise, having put this right-hand vertex into this position, we again make a horizontal truncation to make this vertex Delzant. We introduce a new right-hand vertex, and proceed in the same manner.
Eventually, we get to the point where the remainder \(R_r\) vanishes so the process terminates (this is essentially the Euclidean algorithm). At this point, the final outgoing edge is pointing in the \((1,0)\)-direction.

By construction, the final outgoing edge is pointing in the direction \(\left(\begin{array}{cc}0&1\\-1&b_r\end{array}\right) \cdots \left(\begin{array}{cc}0&1\\-1&b_1\end{array}\right) \left(\begin{array}{c}P\\Q\end{array}\right)\) so we have \[\left(\begin{array}{c}P\\Q\end{array}\right)=\left(\begin{array}{cc}b_1&-1\\1&0\end{array}\right) \cdots \left(\begin{array}{cc}b_r&-1\\1&0\end{array}\right) \left(\begin{array}{c}1\\0\end{array}\right).\] This means that \(P/Q\) has continued fraction \([b_1,\ldots,b_r]\). To see this, note that \[\left(\begin{array}{cc}b&1\\-1&0\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}by-x\\y\end{array}\right)\] and, thinking of vectors as fractions (first entry over second) \[(bx-y)/x=b-\frac{y}{x},\] so if \(x/y=[b_1,\ldots,b_r]\) then \((bx-y)/x=[b,b_1,\ldots,b_r]\). In other words, multiplying a vector \((x,y)\) by the matrix \(\left(\begin{array}{cc}b&1\\-1&0\end{array}\right)\) yields a new vector \((x',y')\) such that the continued fraction of \(x'/y'\) is obtained from that of \(x/y\) by appending a \(b\) at the beginning.