3.02 Quotient topology: continuous maps
Below the video you will find accompanying notes and some pre-class questions.
- Previous video: 3.01 Quotient topology.
- Next video: 3.03 Quotient topology: group actions.
- Index of all lectures.
Notes
Maps from a quotient space
(0.14) Suppose that \(X\) is a space, \(\sim\) is an
equivalence relation on \(X\), and \(Y\) is another space. Given a
map \(F\colon X\to Y\) we say \(F\) descends to the quotient
if there exists a map \(\bar{F}\colon X/\sim\to Y\) such that
\(F=\bar{F}\circ q\), where \(q\colon X\to X/\sim\) is the quotient
map.
(1.47) \(F\) descends to the quotient if and only if \(F(x)\)
depends on \(x\) only through its equivalence class \([x]\), that is
if and only if \[x_1\sim x_2\Rightarrow F(x_1)=F(x_2).\]
(3.07) Conversely, given a map \(G\colon X/\sim\to Y\), we can precompose with \(q\) to get a map \(F:=G\circ q\colon X\to Y\). In other words, \(\bar{F}=G\). This means that:
Functions on the quotient space \(X/\sim\) are in bijection with
functions on \(X\) which descend to the quotient.
Continuity of maps from a quotient space
(4.30) Given a continuous map \(F\colon X\to Y\) which descends to
the quotient, the corresponding map \(\bar{F}\colon X/\sim\to Y\) is
continuous with respect to the quotient topology on
\(X/\sim\). Conversely, given a continuous map \(G\colon X/\sim\to
Y\), the composition \(F=G\circ q\colon X\to Y\) is continuous and
descends to the map \(\bar{F}=G\) on the quotient.
(6.48) For the converse, if \(G\) is continuous then \(F=G\circ
q\) is continuous because \(q\) is continuous and compositions of
continuous maps are continuous.
This will be extremely useful in future: to specify a continuous map
on a quotient space \(X/\sim\), we just need to specify a continuous
map on \(X\) and check it descends to the quotient.
(7.33) If \(F\) is a continuous map which descends to the quotient then, given an open set \(V\subset Y\), the preimage \(\bar{F}^{-1}(V)\) is open in the quotient topology on \(X/\sim\) if and only if \(q^{-1}(\bar{F}(V))\) is open in \(X\) (by definition of the quotient topology). But \[q^{-1}(\bar{F}^{-1}(V))=(\bar{F}\circ q)^{-1}(V)=F^{-1}(V)\] since \(F=\bar{F}\circ q\). But \(F^{-1}(V)\) is open because \(F\) is continuous.
Pre-class questions
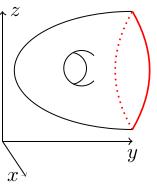
- Let \(X\) be the space in the figure below (thought of as sitting
inside \(\mathbf{R}^3\)) and let \(A\) be the red subset. Which of
the following functions \(X\to\mathbf{R}\) descends to the quotient
\(X/A\)?
- the projection to the \(z\)-axis,
- the projection to the \(x\)-axis,
- the projection to the \(y\)-axis?
Navigation
- Previous video: 3.01 Quotient topology.
- Next video: 3.03 Quotient topology: group actions.
- Index of all lectures.