5.01 Van Kampen's theorem

Below the video you will find accompanying notes and some pre-class questions.

Next video: Fundamental group of a CW complex.
Index of all lectures.

Notes

Van Kampen's theorem

(0.00) Let

$X$ be a topological space and let

$U,V\subset X$ be open subsets such that

$U\cap V$ is nonempty and path-connected. Let

$x\in U\cap V$ be a basepoint. Then

$\pi_1(X,x)=\pi_1(U,x)\star_{\pi_1(U\cap V,x)}\pi_1(V,x).$

(1.12) Here,

$A\star_C B$ denotes the amalgamated product. Suppose you have groups

$A,B,C$ and homomorphisms

$f\colon C\to A$ and

$g\colon C\to A$ . In our case,

$A=\pi_1(U,x)$ ,

$B=\pi_1(V,x)$ and

$C=\pi_1(U\cap V,x)$ , the map

$f$ is the pushforward map

$i_*$ where

$i\colon U\cap V\to U$ is the inclusion, and

$g$ is the pushforward

$j_*$ where

$j\colon U\cap V\to V$ is the inclusion.

(2.33) Given $A,B,C,f,g$ , you can define the amalgamated product

$A\star_C B=\langle\mbox{generators of }A,\ \mbox{generators of }B\ | \mbox{ relations of }A,\mbox{ relations of }B,\mbox{ amalgamated relations}\rangle.$ The amalgamated relations come from elements

$c\in C$ : each

$c\in C$ gives a relation

$f(c)=g(c)$ .

Amalgamated relations

(4.30) What does this mean? We have $f(c)\in A$ and we have already in the presentation of $A\star_C B$ the generators and relations of $A$ , so I can make sense of the element $f(c)$ in the amalgamated product. Similarly, $g(c)\in B$ and we can think of this as an element in the amalgamated product. The corresponding amalgamated relation is just saying that these two elements agree.

(5.13) Geometrically, in the context of Van Kampen's theorem, $C$ consists of loops living in the intersection $U\cap V$ ; the amalgamated relations are then saying ``you can think of these loops as living in $U$ ; you can think of them living in $V$ ; it makes no difference''.

Examples

(5.50) The 2-sphere

$X$ can be written as

$U\cup V$ where

$U$ is a neighbourhood of the Northern hemisphere and

$V$ is a neighbourhood of the Southern hemisphere. The overlap

$U\cap V$ is an annular neighbourhood of the equator. Van Kampen's theorem tells us that

$\pi_1(X)=\pi_1(U)\star_{\pi_1(U\cap V)}\pi_1(V)$ .

We have $\pi_1(U)=\pi_1(V)=\{1\}$ as both $U$ and $V$ are simply-connected discs. Since $U\cap V$ is homotopy equivalent to the circle, $\pi_1(U\cap V)=\mathbf{Z}=\langle c\rangle$ (i.e. one generator, $c$ , and no relations).

The amalgamated product $\pi_1(U)\star_{\pi_1(U\cap V)}\pi_1(V)$ has the empty set of generators coming from $\pi_1(U)$ and the empty set of generators coming from $\pi_1(V)$ . Therefore it has no generators and the amalgamated product is trivial.

(9.07) The fact that $\pi_1(U\cap V)$ is nontrivial doesn't affect this computation: it would only enter into the relations in the group. Indeed, for each $c\in\pi_1(U\cap V)$ , we have $i_*c=1\in\pi_1(U)$ and $j_*c=1\in\pi_1(V)$ , so the amalgamated relations all become $1=1$ , which we don't need to include as a relation because it holds in any group.

The upshot of all of this is the statement that $\pi_1(S^2)=\{1\}$ .

(9.56) Let

$X=S^1\vee S^1$ be the wedge of two circles (i.e. the disjoint union of two circles modulo an equivalence relation which identifies one point on the first circle with one point on the second. We take

$U$ to be a neighbourhood of the first circle and

$V$ to be a neighbourhood of the second. The intersection

$U\cap V$ is a cross-shaped neighbourhood of the point where the two circles intersect (the wedge point).

(10.37) Since $U\simeq S^1$ and $V\simeq S^1$ we have $\pi_1(U)=\pi_1(V)=\mathbf{Z}$ . Moreover, $U\cap V$ is contractible, so $\pi_1(U\cap V)=\{1\}$ . The amalgamated product has a generator $a$ coming from $\pi_1(U)$ and a generator $b$ coming from $\pi_1(V)$ . There are no relations coming from $\pi_1(U)$ , none coming from $\pi_1(V)$ and also no amalgamated relations (since $\pi_1(U\cap V)$ is trivial).

(11.57) A presentation for $\pi_1(S^1\vee S^1)$ is therefore

$\langle a,b\rangle$ . This has no relations: we call a group with no relations a free group on its generators. The elements of a free group

$\langle a,b\rangle$ are words on its generators, written using

$a$ s,

$b$ s,

$a^{-1}$ s,

$b^{-1}$ s, for example

$a^2b^{-1}a^{14}bab^2.$ The only simplifications one may perform with these elements are things like

$aa^{-1}=a^{-1}a=1$ or

$bb^{-1}=b^{-1}b=1$ . In particular, the free group on two generators is not abelian (the relation

$ab=ba$ does not hold).

(13.32) Let

$X=T^2$ , thought of as a square with its opposite sides identified. Let

$U$ be an open disc in the middle of the square. Let

$V$ be (a small open thickening of) the complement of

$U$ . The intersection

$U\cap V$ is a circle. We have

$\pi_1(U)$ is trivial, as $U$ is a disc;
$\pi_1(U\cap V)=\mathbf{Z}$ ;
$\pi_1(V)=\langle a,b\rangle$ , as $V\simeq S^1\vee S^1$ .

To see

$V\simeq S^1\vee S^1$ , note that the square minus a disc is homotopy equivalent to the boundary of the square, which becomes a wedge of two circles in the quotient space.

(16.03) Van Kampen's theorem then tells us $\pi_1(T^2)=\langle a,b\ |\ i_*(c)=j_*(c)\rangle$ , where

$c\in\mathbf{Z}$ is a generator,
$i_*\colon\mathbf{Z}\to \{1\}$ is the trivial map,
$j_*\colon\mathbf{Z}\to\langle a,b\rangle$ sends a generator for $\mathbf{Z}$ to some word in $a,b$

(16.37) This amalgamated relation

$j_*(c)=1$ can be read from the picture: the boundary of the circle is homotopic to the loop

$b^{-1}a^{-1}ba$ in

$V$ . Therefore the amalgamated relation for the generator

$c\in\mathbf{Z}$ is

$1=b^{-1}a^{-1}ba$ .

(18.00) This relation is equivalent to $ab=ba$ , so the group we get is just the abelian group $\mathbf{Z}^2$ .

Pre-class questions

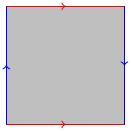
The Klein bottle $K$ is obtained from a square by identifying opposite sides as in the figure below. By mimicking the calculation for $T^2$ , find a presentation for $\pi_1(K)$ using Van Kampen's theorem.

Navigation

Next video: Fundamental group of a CW complex.
Index of all lectures.