KIAS Workshop
This was helped by the structure of the workshop: over the course of the week, there were only eight speakers, each giving two or three talks. This encouraged speakers to take time explaining illustrative examples and background, rather than rushing over these to try and state their theorem within an hour.
Here are a couple of the things I learned (in this case, specifically from the lectures of Hakho Choi).
First thing
Recall that the lens space \(L(n,a)\) is the link of the cyclic quotient singularity of type \(\frac{1}{n}(1,a)\). Lisca classified minimal symplectic fillings of lens spaces (equipped with their Milnor fillable contact structures). The result was that all fillings are diffeomorphic to Milnor fibres of cyclic quotient singularities. This much, I knew.
Shamefully for someone who has spent so much time the last few years thinking about these spaces, I didn't know that this result had been strengthened by Bhupal and Ono, so it is now known to be a classification up to symplectic deformation equivalence (i.e. any minimal symplectic filling can be deformed until it is symplectomorphic to one of these (exact) Milnor fibres).
Second thing
Choi was talking about a result from his paper joint with Jongil Park in which they classify fillings of certain other Seifert fibred 3-manifolds using methods similar to Lisca and Bhupal-Ono. The result is that the symplectic fillings (up to deformation) are obtained by iterated (generalised) rational blowdown from the minimal resolution of the corresponding singularity. For lens spaces, this was proved by Bhupal and Ozbagci in their beautiful paper on planar Lefschetz fibrations on fillings of lens spaces; Choi also has a paper joint with Park and Shin where they prove this result using MMP.
Now... The result I knew before about classifying fillings of lens spaces is that they can all be obtained by (noniterated) generalised rational blow-down from the maximal resolution defined by Kollar and Shepherd-Barron (that is, you contract and smooth a bunch of disjoint Wahl chains). The maximal resolution is obtained by blowing up the minimal resolution as much as you can while still keeping the property that the canonical class evaluates positively on all the proper transforms of the exceptional curves of the minimal resolution. I discussed this in my own lectures at the workshop.
There is a point of view on these symplectic fillings that I personally like, which is that they are almost toric manifolds specified by some 2-dimensional polygon with decorations. This point of view is also explained in my lecture notes. I wanted to understand the Bhupal-Ozbagci/Choi-Park-Shin result from this point of view.
Rational blow-down is a surgery which takes a certain chain of spheres and replaces a neighbourhood of them with a rational homology ball. If you want to perform rational blow-down iteratedly (i.e. blow-down a rational blow-down) then you need to be able to find chains of spheres in the surgered manifold. I had the impression this was nontrivial, but it turns out that you can see these chains of spheres very easily in the almost toric pictures.
The minimal resolution is actually toric: the moment polygon is a truncation of a certain wedge in the plane by a sequence of lines of increasing slope. You start by picking a suitable (Wahl) chain of spheres from amongst the toric divisors. Rationally blowing down means changing the toric polygon to contract these edges, and then inserting a decoration. The decoration consists of a marked point in the polygon (over which there now lives a singular Lagrangian torus fibre) and a branch cut connecting this point to the vertex obtained by contracting the edges. This is a branch cut for the integral affine structure you get on the almost toric diagram; with respect to this integral affine structure, the two edges on either side of this special vertex actually form a straight line (which just happens to pass through a branch cut). Therefore the preimage of these two lines is again a symplectic sphere, which you can use as part of a subsequent Wahl chain to rationally blow down again.
In examples, you can now use this to produce the iterated sequence of rational blowdowns needed for all the different symplectic fillings.
- I'll write a chain of numbers, some of which are encircled by brackets;
- the numbers represent (minus the) self-intersections of spheres in a chain.
- the bracketed expressions are sub-chains, which, if rationally
blow-down give the relevant filling.
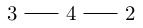
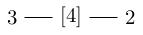
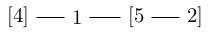
In this last case you can see why we sometimes need to go to the maximal resolution if we want to explain things using a noniterated rational blowdown in a bunch of disjoint Wahl chains.
Now let's see how to get the last example by iterated rational blow-down of the minimal resolution. The toric picture of the minimal resolution is:
where we label edges by a vector parallel to them. Rationally blowing down the central \(-4\)-curve, which lives over the edge parallel to \((3,1)\), we get: