How not to prove the concurrent normals conjecture
The concurrent normals conjecture (Problem A3 in Croft, Falconer
and Guy "Unsolved problems in geometry") is a basic statement in
Euclidean geometry which remains open in dimensions \(\geq 5\)
despite the best efforts of mathematicians. Here I explain some
things I tried which failed.
Read on for more...
Video feedback
In the Autumn Term 2020, I tried using video feedback on
students' homeworks. I wrote a short piece about it for
Lancaster's "Embrace Digital" website, but it seems like you
need to log in to see it. So for anyone who isn't at Lancaster,
here's a summary of what I wrote.
Read on for more...
Teaching online (April 2020)
I've been producing lots more lecture notes and videos (this time for
MATH105 Linear Algebra). You can see the results
here. I decided to
update the lzl.py script that I use to produce these notes to allow me
to add alt tags to images (to make my notes more accessible). The
latest version on github has this functionality.
To complement these videos/notes, I'm currently running live sessions
for MATH105 using M*crosoft Teams (that's what Lancaster uses, and to
be fair it is going pretty smoothly). I use my trusty Wacom Bamboo
tablet and pen to run through worked examples/solutions and to field
questions from the students; I have a team of tutors on hand to help
monitor the chat and contribute. I'm finding this a fun experience:
many students seem more ready to interact using chat than they do in
real life in a lecture theatre. I'm also able to run polls more easily
in an online setting (getting them to vote on different options in
chat by "liking" them) so multiple choice questions seem to be going
down quite well. This week I'm going to try using "breakout rooms",
which might be a step too far in complication.
Of course, it's very hard for me to know what the student experience
is like. I'm hoping to get some feedback from students at the end of
this week, so we'll see if this is as much fun for them as it is for
me.
Next year, if all goes to plan and the world doesn't end, I will be
teaching Lie groups at Lancaster. I plan to flip this too (this was my
plan even before COVID-19 reared its ugly head), so more video
lectures are imminent...
Fukaya categories 1: What is Floer theory?
If you have never come across the amazing ideas of Andreas Floer, the
definition of a Fukaya category will seem almost completely
unmotivated. In the words of the famous joke, "If I were going there,
I wouldn't start from here." So for those of you who haven't seen
Floer theory before, I'm going to start by reviewing the basics. To
avoid getting hung up on technicalities, the review will be at a
cartoon level of rigour; I will become more rigorous later when I
specialise to the setting I want to use (exact Lagrangians in
cotangent bundles).
Read on for more...
Fukaya categories
This term, we will be running a reading group at Lancaster in the
algebra/geometry group. We will be focusing on various topics,
including Fukaya categories, derived localisation, Koszul duality
(amongst other things!). I have promised to talk about Fukaya
categories until the audience gets sick of it (which may happen sooner
rather than later). I'm planning to post notes of what I say here (in
case someone misses a session and needs to catch up).
Postdoc wanted
We are advertising an 11 month postdoc position in symplectic topology
and/or algebraic geometry at Lancaster University in the beautiful
North-West of England:
here is the application page. This is funded by
(what's left of) my
EPSRC
grant "Singularities and Symplectic Topology". Starting date 1st
January or as soon thereafter as convenient. If you're interested in
applying, let me know (j.d.evans at lancaster.ac.uk).
See the vacancy page for more information.
KIAS Workshop
Earlier this summer, I spent a week in Seoul at the Korean Institute
for Advanced Study (KIAS) at a workshop on
"Algebraic and Symplectic
Aspects of Degenerations of Complex Surfaces" organised by Professors
Dongsoo Shin, Heesang Park, JongHae Keum and Giancarlo
Urzúa. It was a fantastic workshop, drawing together
researchers from very different backgrounds (MMP and algebraic
geometry, symplectic topology/holomorphic curves, low-dimensional
topology, toric geometry/deformation theory) and getting us to make
our work accessible to one another, emphasising the connections
between the different threads and the unity of what we are doing. In
that, it was enormously successful.
This was helped by the structure of the workshop: over the course of
the week, there were only eight speakers, each giving two or three
talks. This encouraged speakers to take time explaining illustrative
examples and background, rather than rushing over these to try and
state their theorem within an hour.
Here are a couple of the things I learned (in this case, specifically
from the lectures of Hakho Choi).
Read on for more...
Why open notebook mathematics?
I want to elaborate more on why I decided to set up an
open notebook
where anybody on the internet can see what I'm working on in
quasi-realtime.
Read on for more...
Scientific communication
In honour of postdoc appreciation week...
Which of the following is the ultimate purpose of scientific
communication?
- To impress expert referees and convince them that you are clever.
- To bolster your publication record.
- To get cited lots.
- To publish in top journals.
- None of the above.
Read on for more...
3-dimensional lightbulb theorem
Recently, Gabai proved a fantastic theorem about knotted surfaces
\(\Sigma\subset S^2\times S^2\). You can read about it in
Gabai's
paper, or in
Edwards's expository paper. The theorem says that if
\(\Sigma\) intersects \(\{p\}\times S^2\) once transversely then
\(\Sigma\) is actually unknotted (i.e. it's isotopic to one of the
standard spheres \(\{(z,z^k)\ :\
z\in\mathbf{C}\cup\{\infty\}\}\)). This is the analogue of a (trivial)
classical unknottedness theorem in 3 dimensions, called the lightbulb
theorem, which I didn't actually know about until I heard about
Gabai's result. In this blogpost, I want to discuss the idea behind
the 3-dimensional lightbulb theorem (I haven't yet understood the
proof of the 4-dimensional version).
Read on for more...
Erratum for arXiv:1110.0927
I said that I would be posting clarifications and errata for my old
papers. Here's another one.
Read on for more.
Open notebook
I have started an
open notebook. It's somewhere I plan to post some of
the mathematical questions I'm thinking about, while I'm thinking
about them, and to post whatever progress I've made on them, while
it's being made. This is quite different from my usual mode of working
(where I think about things for a year or more and then eventually
write up the distillate and post it to arXiv).
Read on for more.
Chain relations
There is a beautiful series of relations in the mapping class groups
of punctured surfaces called the
chain relations. In this post,
I will explain the origin of these relations in algebraic geometry.
Read on for more.
manim
[2019-06-21 Fri]
I recently taught a linear algebra class. Before I taught it, Momchil
Konstantinov recommended I check out the Youtube channel 3Blue1Brown
(produced by Grant Sanderson), which apparently had some nice videos
about linear algebra. I was too busy preparing to teach. Once marking
the exam was over, I thought I would relax by taking his advice and
seeing someone else's take on linear algebra.
My mind was blown.
Read on for more.
First things first
Once upon a time I was summoned for an interview with GCHQ about a
summer internship. Given that I have never done a summer internship
with GCHQ, you can already tell that this interview did not go
well. However, I learned something useful from this interview about
problem-solving which I would like to share with you.
Read on for more...
Mathematical reading
This used to be a random page on my website, but I thought I would
incorporate it into my blog.
A big part of the practice of mathematics is the struggle to put our
own internal mathematical universes into order, trying to fit new
understanding in with old.
To do this by reading what other people have written is difficult,
because their way of structuring things can be very different from the
way you think.
Here are some of the things I keep in mind when trying to read things
other people have written.
Read on for more...
Am I allowed?
I notice more and more these days that students ask me "Am I allowed
to..." For example, "am I allowed to use row-swapping to solve this
question?" or "am I allowed to use cross products to find this
vector?". Maybe cross products were covered in a different course, or
maybe I introduced row-swapping after the other row operations to
avoid talking about signs in determinants early on.
The question really means: "Will I lose marks for doing this?" which
is a perfectly legitimate question. However, it is a clear example of
educational "backwash", where the means of teaching or assessing has a
negative impact on the way students learn.
Read on for more...
Small resolutions
Recall that if \(X\) is a singular variety then a resolution of \(X\)
is a morphism \(\tilde{X}\to X\) from a smooth variety to \(X\) which
is an isomorphism outside the singular locus. The exceptional locus of
a resolution is the preimage (in \(\tilde{X}\)) of the singular locus
in \(X\). A resolution is "small" if the exceptional locus has
codimension bigger than 1. The classic example of this (which I
discussed years ago in
another blog post) is the small resolution of
the 3-fold ordinary double point, where the small resolution replaces
the singular point with a copy of \(\mathbf{CP}^1\) (which then has
complex codimension 2 in the 3-fold).
I was discussing all of this with my collaborator Mirko Mauri and
trying to understand when small resolutions exist in more complicated
situations. He told me something which blew my mind. "Small resolutions
often occur when you blow up a divisor." Don't be silly, I said,
blowing up a divisor doesn't do anything. He pointed out that blowing
up a Cartier divisor doesn't do anything, but blowing up a Weil (but
non-Cartier) divisor can do something. At this point, I was trying to
remember what the difference was and whether all Cartier divisors were
Weil or vice versa or neither. By the end of our discussion, I had a
much better understanding of what "blowing up a divisor" means from
the viewpoint of a symplectic geometer. I try to explain this below.
Read on for more...
Associahedra
I had a fun conversation about associativity the other day with one of
our first year students who is taking my linear algebra class. This
blog post is inspired by that conversation.
Mathematicians are big on proofs. We like to work out every tiny
detail of an argument before presenting it to the world. Sometimes
this can seem like pedantry, and doubtless there are mathematicians
who are pedants. But I would like to argue that this process of
carefully examining the minutiae of an argument can lead one to new
and unexpected discoveries. This is completely analogous to the way
that a scientist, confused by discrepancies between theory and
experiment, can find a new, deeper theory by careful and imaginative
examination of the basic assumptions of the old theory.
I'm going to introduce a mathematical idea which will seem, at first
sight, pretty boring. Then I'll show you how it leads you naturally to
something completely unexpected.
Read on for more...
Moving
In little under a month, I'll be leaving London and UCL and joining
the
Mathematics Department at
Lancaster University. I will be a member
of
Grizedale College. It has long been a dream of mine to return to
the
North of England, and I'm very excited about it.
I have had a wonderful seven years at UCL: it is an incredibly
friendly place with an abundance of excellent and motivated students
and researchers. Thank you to everyone who has made my time here so
enjoyable.
Note that this means that my website will be moving too, so if there
are people out there who occasionally read this blog or use the
resources on my website, be warned!
Undergraduate pathways update
Some years ago, I wrote some graphviz files which generated dependency
graphs for our undergraduate course at UCL, to help students figure
out which modules were available and what the prerequisites were. The
files were not so easy to maintain, so I recently wrote some code to
automate the production of these images. The idea is that all the
information about the course and module dependencies is contained in a
relatively-easy-to-read-and-edit XML file and that some XSL transforms
are then used to convert it to graphviz. Admittedly, XSL being a very
verbose functional language, the transforms themselves are not the
easiest thing to maintain, but I have always liked the W3C's vision of
the semantic web so I went with it anyway. For example, it would be
natural to use the XML file to store other information like syllabus
content, and then generate syllabus pages/LaTeX files automatically
using another XSL transform. You can see the code
here and the webpage
with the images
here.
Developing map
Following on from my last post, here are more figures that will appear
in my lectures on Lagrangian torus fibrations. This time, we see the
image of the developing map for the integral affine structure for the
base of a Lagrangian torus fibration on \(\mathbf{CP}^2\) obtained
from the standard ``moment triangle'' by (a) one, (b) two, and (c)
three nodal trades. The result is the union of all mutations of the
moment triangle, which gives a rather lovely ``integral affine
fractal'' in the plane. For me, mutations always seemed a little
mysterious until I thought of drawing a picture like this. The point
is that action coordinates are not globally defined on the base of a
Lagrangian torus fibration, they only really make sense on its
universal cover. When you look at two polygons related by a mutation,
you're really looking at the image of two neighbouring fundamental
domains in the universal cover under action coordinates.
Read on for more...
Focus-focus singularities
I am currently giving a graduate-level lecture course on Lagrangian
torus fibrations. One of the side-products of this is some images
which I have generated using a computer and which I want to display in
class. The lectures are being held outside of the university, so it
costs extra to hire a projector, and I am not using a projector for
the majority of the lectures, so instead I will post these images to
this blog and direct students to look at them using their mobile
devices (or the mobile device of their neighbour, if they don't have
one).
The images illustrate the developing map for the integral affine
structure on the base of a Lagrangian torus fibration in the
neighbourhood of a focus-focus fibre.
Read on for more...
Elliptic function slide rule
In the early hours of this morning, I was lying awake in bed thinking
about slide rules (as one does) and imagining how a slide rule for
Jacobi's elliptic functions might look. I realised that there is a
nice picture associated with this, which illuminates what the Dehn
twist has to do with elliptic functions.
Read on for more...
Fanography
If you're anything like me, you often find yourself wishing that the
Fano-Iskovskikh-Mori-Mukai classificiation of Fano 3-folds were
readily available to browse online and that the data were also
available in a format which could be processed by computer.
Both such a database and a YAML file from which the database is
generated are now available thanks to the efforts of Pieter Belmans.
Flipping conclusion
As I posted before (
here and
here), I tried flipping my lecture course
Topology and Groups this year (2018). This meant converting my lecture
notes into a sequence of online videos with accompanying notes (each
lasting approximately 15-20 minutes) and converting my problem sheets
into worksheets we would work through in class. Each week, the
students have been required to watch about 90 minutes of videos and
then in class we have worked through the worksheets, focusing on
examples, group-work and discussion, which is supposed to support the
learning from the videos. In this blog post I will summarise what I
have learned from the experience.
Read on for more...
Flipping update
As I wrote in an earlier post, I'm planning to flip my lectures for
next year. I'm currently in the act of recording videos for my
lectures. After experimenting with a number of different techniques
for this over the years, I've finally hit on a setup I like that works
well with Linux.
Read on for more...
Mathematical bookbinding
Some problems:
- Maths books are expensive.
- Printing papers out is usually a waste; I lose track of which papers
I have printed and they mount up in enormous, disorganised,
dog-eared piles on my desk. I sometimes find it fun to work my way
downwards through one of these piles, and see the stratified history
of what I have been thinking about for the last year. But it's not a
sensible way to organise one's life.
- Screen-readers are just not the same... I got an iPad a few years
ago so I could minimise printing, and it's very convenient to carry
around all my papers in electronic form. But still, I find it very
difficult to focus in depth on something I'm reading on a screen. I
like to be able to flick through and hold different pages open. I
like books.
So I recently took up bookbinding and I'm making my own hardback
mathematics books out of freely available PDFs online (books or
research papers that I've been meaning to read properly). This is not
difficult, so I thought I'd share some of my experiences below.
Read on for more...
Cyclic quotient singularities, II
This is the second of my posts covering background material on cyclic
quotient singularities of surfaces which I find myself looking up or
working out from first principles on an almost daily basis at the
moment (
the first one is here). In this post, I will discuss
discrepancies and intersection numbers in surfaces with singularities,
and explain how to compute them.
Read on for more...
Cyclic quotient singularities, I
I have been reading the paper
"Flipping surfaces" by Hacking, Tevelev
and Urzúa, which is a detailed study of a certain class of 3-fold
flips. There is some background material about cyclic quotient surface
singularities which I keep having to figure out from first principles
whenever I return to this stuff and it would be helpful to have it
written down somewhere. To that end, here is the first in a series of
posts about this, covering the toric model for cyclic quotient
singularities and the minimal resolution.
Read on for more...
Horikawa surfaces
Mostly for my own convenience, here is an overview of the geometry of
Horikawa surfaces (because I will forget most of this).
Read on for more...
New blog functionality
At the behest of
Pieter Belmans, I have now added an
RSS feed to the
blog to make it easier for people to follow. I have also added a
blogroll.
Here is the shell script which I
used to generate the RSS feed for the blog.
This script is not without its flaws. For example, if a blog post is
only on the index page and doesn't have as separate file to link to, I
have just linked to the blog index (I should really include an anchor
to link to... maybe another day). Probably, I should use ox-rss or
some other elisp solution, but I find shell scripts easier to deal
with.
One more piece of fun: I recently acquired an Android smartphone (so
that I could send photos of my new baby to his grandparents via
whatsapp). I became much more enamoured of this phone when I realised
I could install a terminal emulator (Termux), use this to install
Emacs and Git, and so I can now make blog posts from my phone.
Farmageddon

I have just finished reading the book Farmageddon by Philip Lymbery
and Isabel Oakeshott. It is the most important book I have read in a
number of years. It is a dazzling journalistic expose of how
industrial-scale agriculture and factory farming has systematically
raped the world's farmlands in the last half century.
Read on for more.
A crib sheet for surfaces
Every time I want to think about complex surfaces, I find I have
forgotten what things like \(q(X)\) and \(p_g(X)\) mean and how they
are related to things like \(c_1(X)\) and \(c_2(X)\). To save me
carrying Barth-Peters-Van de Ven around with me, here is a blog post
containing the basic definitions.
Update: See also this page of Pieter Belmans and Johan Commelin
for an interactive complex surface explorer!
Read on for more.
Clarification for arXiv:1606.08656
The paper Ivan Smith and I wrote on Lagrangian pinwheels in
\(\mathbf{CP}^2\) and Markov numbers has recently appeared in
Geometry and Topology. Shortly thereafter, Yong-Geun Oh
contacted us with some excellent questions where our exposition was
less than clear. In case anyone else has the same questions, I thought
I would write a blog post clarifying these points.
Read on for more.
Clarifications and errata
In the spirit of
Michael Hutchings and
Paul Seidel, I have decided to use
this blog to keep track of clarifications and errata for my
papers. Most of my papers say something wrong or inaccurate but
nonfatal. In most cases, it doesn't seem worth filing a
correction. But occasionally someone asks me about one of these things
and, it being several years since I wrote the paper, I panic all over
again trying to figure out why their question doesn't invalidate my
work (piece of advice: when this happens to you, almost always trust
your past self; they were much more familiar with the paper when they
were writing it). I will keep the list below updated as I add more
clarifications and errata to the blog.
Read on for more.
Flipping
I have decided that next year I am going to try lecture-flipping my
topology module. Lecture-flipping is the practice whereby the lecturer
prepares material for the students to view/read ahead of time, and the
lecture is spent getting the students to explore the material in more
depth and consolidate their understanding. I have decided to document
my experience in case it's useful for other people thinking about
flipping (specifically in the context of maths lectures).
In this blog post I want to review:
- why on earth I'm planning to do this,
- what it means in practice,
- what I've already done.
Read on for more.
TikZ and org-mode
As an org-mode newbie, it took me a while to figure out how to get
TikZ code in my source files to generate images in my blog. This blog
post explains the solution I found.
Read on for more.
Noether's theorem in field theory
This blog post attempts to explain Noether's theorem in field theory
(including Noether currents) in a way that might appeal to a
mathematician familiar with symplectic topology and the Hamiltonian
formalism. Hopefully someone will find it useful...
Read on for more.
The Heisenberg picture and causality
This blog post summarises what we learned about propagators and
causality in free scalar QFT.
Read on for more.
What is a quantum field?
As a mathematician trying to learn QFT, a question that always
bothered me was "what is a quantum field?". This blog post explains
one point of view (the Schrödinger picture) on the answer to this
question which I find satisfying.
Read on for more.
Pre-QFT 1: the quantum harmonic oscillator
The archetypal physical system is the simple harmonic oscillator: a
ball on a spring following Hooke's law follows periodic motion along a
circle in phase space (its displacement and momentum oscillate
sinusoidally between two extremes and out of phase like sin and
cos). Understanding the corresponding quantum system is fundamental to
understanding quantum field theory: indeed, quantising a free
(bosonic) field turns out to be equivalent to quantising an infinite
collection of simple harmonic oscillators.
Read on for more.
Quantum field theory reading group
Like many people, I got into maths because I was interested in quantum
field theory and didn't understand what was going on. I have spent a
lot of time idly browsing QFT textbooks over the years in an effort to
rectify this, but stuff always got in the way.
Ed Segal and I are planning to run a QFT reading group at UCL to
improve our understanding. I will post my own notes from the reading
group to this blog, as well as some foundational "pre-QFT" material
which I always forget and have to re-read whenever I start looking
into this stuff after a long break.
If you are interested in attending the reading group, please let Ed or
me know.
Equivalence relations
Equivalence relations are an important concept in mathematics, but
sometimes they are not given the emphasis they deserve in an
undergraduate course. Having a good grasp of equivalence relations is
very important in the course MATHM205 (Topology and Groups) which I'm
teaching this term, so I have written this blog post to remind you
what you need to know about them. I will kick off with a few examples,
then give a more formal definition.
Read on for more.
Theorem and proof environments in CSS
Here is a nice idea from
Dr Z.ac, the blog of Zachary Harmany. You can
use CSS to create LaTeX-style theorem/proof environments on a website.
Read on for more.
Connecting to wifi from command line
I so rarely need to connect to a new wifi network that, when I do, I
always forget how I managed to do it the previous time. For future
reference, here's how I did it this time (using "NetworkManager
Command Line Interface" or "nmcli"):
$ nmcli dev wifi list
$ nmcli dev wifi connect NETWORKNAME password NETWORKPASSWORD
New blog
I've decided that I don't like my old blog and I'm setting up a new
blog using org-mode.
Read on for more.
Resonances
How could you "detect" a new subatomic particle, given that it's so
small you can't see it and (often) so short-lived that you'd miss it
even if you didn't blink?
Read on for more.
Nice paper bump
It's 7 years old, but I only just came across the following
beautiful
expository paper of Baez and Hurta on the representation theory
underlying the standard model and grand unified theories and I thought
I would give it a bump. It overlaps with some of the material I touch
on in the Lie Groups course I teach (using representations to classify
particles) but goes into much more gorgeous detail and focuses on
fundamental particles rather than baryons/mesons. It is unusually easy
to follow (if you know a bit of representation theory) and I learned a
lot from reading it.
Is the speed of light constant?
I recently came across
a beautiful argument due to De Sitter (1913),
which gave the (first?) experimental evidence that light moves with a
constant speed.
Constancy of the speed of light is one of those things that always
bothered me, and I spent a couple of days recently trying to unbother
myself. De Sitter's argument is what finally satisfied me. Below, I’m
going to explain the background, then I'll explain De Sitter's
argument. The De Sitter paper is only a couple of paragraphs long and
is available via Wikisource, so if you don't need the introductory
remarks in the blogpost below, just follow the link above and read it.
Read on for more.
Using graphviz to illustrate course structure
At some point last year, I got frustrated that I couldn’t see easily
the global structure of the UCL undergraduate maths course without
trawling through a bunch of PDFs, so I made a webpage to illustrate
it. Hopefully some people have found this useful in deciding which
modules to choose or in advising students which modules to take.
Update (3rd Feb 2018): I have now updated the source code for this to
make it easier to maintain. It is now available on GitHub.
Some simple spectral sequences
I keep finding myself trying to explain how the very simplest spectral
sequences arise (spectral sequence to compute the cohomology of a cone
or an iterated cone), so I have taken the time to TeX the explanation
into a
sequence of guided exercises. This is all very formal and
diagram-chasy. One of the off-putting things about spectral sequences
is all the indices; in these exercises I have suppressed gradings and
concentrated on the very simplest cases to avoid overcomplicating the
notation. Once you’ve seen how the proof goes, you should go and look
in Bott-Tu or McCleary for some actual examples and computations.
Please let me know of any errors in the exercises!
A sanity check for the Fukaya category of a cotangent bundle
Yesterday I gave a seminar about Fukaya categories and I didn't have
chance to do quite as much explicit computation as I'd hoped. I
thought I’d write a blog post with a basic calculation to show you the
kind of things that are involved in doing computations in Fukaya
categories. I will show (using Abouzaid's description of the zero
section in terms of the cotangent fibre) that the zero section and the
cotangent fibre have \(rank(HF) = 1\), in the special case of
\(T^*S^1\). This is such a trivial result in the end (you could do the
computation just by looking at the intersection and seeing it's a
single point) that you should think of this post as more of a sanity
check.
Read on to test your sanity.
Cone eversion
Last year, around the time Chris Wendl was running the h-principle
learning seminar at UCL, I set my second years an exercise from
Eliashberg-Mishachev as a difficult challenge problem: to find an
explicit cone eversion. In other words, find a path in the space of
functions on \(\{(r,\theta)\in\mathbf{R}^2\ :\ r\in[1,2]\}\) connecting
\(r\) to \(2-r\) such that none of the intermediate functions has a
critical point. One of these students, Tom Steeples, got hooked on the
problem, almost solved it, and afterwards used Mathematica to produce
some beautiful computer animations of a solution given by Tabachnikov
in American Mathematical Monthly (1995) Vol 102, Issue 1, pp
52–56. Here is one of his images. Reproduced with Tom's kind
permission (the copyright is his).
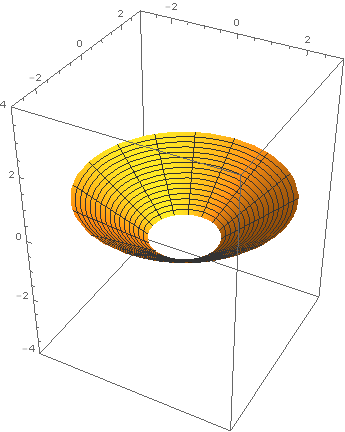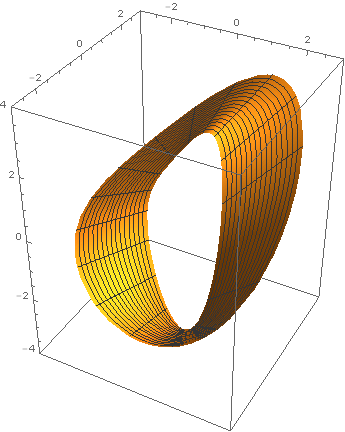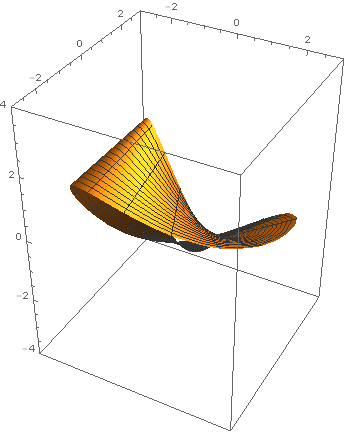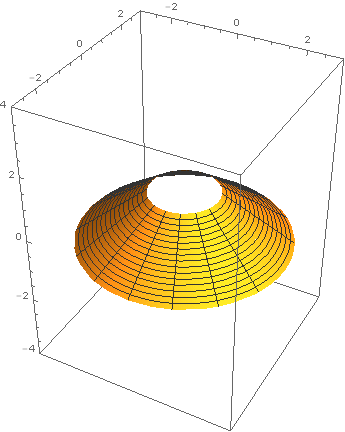
Gromoll filtration
In my
latest preprint with Georgios Dimitroglou Rizell, we use the
topology of diffeomorphism groups of high-dimensional spheres to
produce interesting examples of nontrivial topology in
symplectomorphism groups of cotangent bundles. Until we started
thinking about this, I didn’t know much about the higher homotopy
groups of \(Diff(S^n)\) so here is some interesting stuff I learned
while we were writing this paper.
Read on for more.
E-learning project report
My final report on the e-learning project "Video lectures filmed by
students" is now
available to download in PDF form.
The purpose of this e-learning project was to test the effectiveness
and viability of getting students to film mathematics lectures and the
effect on student learning of making these videos available. The
project was made possible by an E-Learning Development Grant (ELDG)
and by the cooperation of a large number of people who I thank at the
end.
Disclaimer. The project analysis is not scientific: there is no
attempt made at comparison with a control group, the data sets are not
large and the statistical methods used to analyse them are crude. This
report is intended to be at best a rough guide to the UCL Mathematics
Departmental Teaching Committee as to what action to take on filming
of mathematics lectures.
December: video project update
The video project has been progressing nicely: all of the videos have
now been compressed and most have been uploaded to either Youtube or
Lecturecast.
Read on for some of the results
Geometry and undecidability
These are the notes from a talk I gave to the UCL Undergraduate
Mathematics Colloquium in early October and I would like to thank them
for being such an attentive audience with so many good questions. The
talk is a gentle introduction to the work of Nabutovsky and
Weinberger, on how logical complexity gives rise to complexity for
sublevel sets of functionals in geometry.
Read on for the rest of this entry.
Video-lecture project weeks 1 and 2
The e-learning project for filming maths lectures is now underway
(into its second week). You can see some of the initial results
here
and
here.
Read on for a summary of the early teething problems we have
experienced and some of the solutions we have found.
E-Learning: Video lectures filmed by students
I recently received a grant from the UCL e-learning team to run a
project for filming maths lectures.
Read on for more about the project.
E-Learning: Spring 2013
Henry Wilton, Bonita Carboo and I are the UCL Maths Department's
e-learning reps. In the interests of sharing ideas, here are a few
things I have discovered this Spring about e-learning which may be
useful to others.
Read on for more.
Bored now
I just read a BBC article about Jimmy Wales called "Boring university
lectures are doomed" and the title and the tone of the article made me
angry. As a boring university lecturer, I felt I should speak out.
Read on for more.
The geometric definition of the Johnson homomorphism
I have recently been thinking about Torelli groups.
The Torelli group of a surface is the subgroup of mapping classes
which act trivially on cohomology. Consider the case of an orientable
surface with \(g\) handles and one boundary component (diffeomorphisms
are required to fix the boundary). There is a famous homomorphism from
this group to the free abelian group of rank \({2g\choose 3}\) called
the Johnson homomorphism. The usual definition is pretty
algebraic-looking (involving the mapping class group action on the
fundamental group and its commutator subgroup). This week I read an
alternative (extremely beautiful, geometric) definition of this
homomorphism in Johnson's survey paper on the Torelli group
(D. Johnson, A survey of the Torelli group, Contemp. Math. (1983)
vol. 20, 165-179). This definition is probably very well-known, but I
didn't formerly know it and I thought it was too nice not to blog
about.
Read on for more.
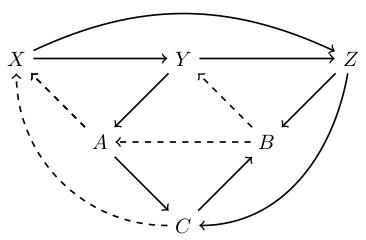
TikZ code for the octahedral axiom
If anyone finds it useful, I've created a LaTeX command for drawing
the octahedral axiom (requires the TikZ package) based on this example
of Stefan Kottwitz. You can easily edit the code to add labels to
arrows (they would go in the empty brackets in the lines that say
"edge") or add these as extra arguments to the function.
Include the following code in the head of your LaTeX document:
\usepackage{tikz}
\usetikzlibrary{arrows}
\newcommand{\Octa}[6]{\begin{center}
\begin{tikzpicture}[node distance=2cm,thick]
\node (1) {\(X\)};
\node (4) [below right of=1] {\(A\)};
\node (6) [below right of=4] {\(C\)};
\node (2) [above right of=4] {\(Y\)};
\node (5) [above right of=6] {\(B\)};
\node (3) [above right of=5] {\(Z\)};
\draw[->] (1) to[out=25,in=155] (3);
\draw[->] (1) -- (2);
\draw[->] (2) -- (3);
\draw[->] (2) -- (4);
\draw[->] (3) -- (5);
\draw[->] (3) to[out=260,in=0] (6);
\draw[->] (4) -- (6);
\draw[dashed,->] (4) -- (1);
\draw[->] (6) -- (5);
\draw[dashed,->] (4) -- (1);
\draw[dashed,->] (5) -- (4);
\draw[dashed,->] (5) -- (2);
\draw[dashed,->] (6) to[out=180,in=270] (1);
\end{tikzpicture}
\end{center}}
Then the command
\Octa{X}{Y}{Z}{A}{B}{C}
will produce a diagram like this:
Convex Integration (talk notes)
In case you were unable to take notes from my talk (either because you
were unable to attend or because you were present) I've written them
up below in some detail. They're basically just a summary of
Borrelli's notes.
Also relevant is the preliminary cartoon which contains many of the
essential ideas.
Warning: Images are large may take some time to load.
Read on for more.
Convex integration (cartoon)
On Thursday I'll be giving a talk on convex integration at the
London
h-principle learning seminar. This will be a dry and technical
subject, so I thought I'd create some light-hearted preliminary
reading. Here then, in cartoon-form, is the simplest version of
1-dimensional convex integration, used to construct an immersed loop
in the plane whose tangent vector has winding number zero.
The technical details of the talk will be heavily based on these notes
by Vincent Borrelli, which is an excellent place to learn all this
stuff from.
Warning: The cartoon is big (about 1MB) and may take time to load.
Read on for more.
Kronheimer's argument: Small resolutions and Dehn twists
I want to amplify an expository argument I gave in
a recent lecture
which shows that the squared Dehn twist on a symplectic 4-manifold is
smoothly isotopic to the identity map. This is an old argument of
Kronheimer and I only managed to sketch it hurriedly in the lecture. A
few people have asked me to explain this to them in the past, so...
Read on for an explanation to which I can point people in future.
Symplectic/Contact Geometry VII at Les Diablerets, Day 1
I'm currently in Switzerland at the seventh
"Symplectic Geometry,
Contact Geometry and Interactions" Workshop funded by
CAST. This is a
yearly conference which started at the same time I started my PhD so I
have a great fondness for these workshops. This one is in the
mountains, which makes me even fonder...

After three excellent talks today I decided to act as a "maths
journalist" and summarise the main ideas from the talks in this
blog. I may not be able to keep this up, as there's six talks tomorrow
and too much snow to enjoy. Today's talks were:
- Urs Frauenfelder "A \(\Gamma\)-structure on the Lagrangian
Grassmannian"
- Yochay Jerby "The symplectic topology of projective manifolds with
small dual"
- Alex Ritter "Floer theory for negative line bundles"
Read on for more...
UCL Geometry and Topology Open Day talk: Floer theory
These are the notes from the twenty minute talk I'm going to give at
the UCL Geometry and Topology Open Day for prospective PhD students
(November 14th 2012). For those who are interested in reading more,
check out Milnor's book on Morse theory and Atiyah's early survey
paper on Floer theory.
Read on for more...
Why Schrödinger's equation?
"Why this equation?"
I recently overheard someone ask this about Schrödinger's
equation. The answer they received was, for me, unsatisfying. "Because
it agrees with experiment." Of course, that answers perfectly why the
equation was adopted by future generations of physicists and indeed
the calculation of the spectrum of atomic hydrogen from the energy
eigenvalues of the Schrödinger operator is one of the most convincing
and wholesome computations a young physicist can do. But the question
that was left unanswered, the question I believe was being asked, was:
"Why did Schrödinger write this equation down? Why not something
else?" I don't believe for a second that Schrödinger sat down with an
array of different equations and worked out what each of them
predicted about hydrogen before he found the one that fit...
Read on to find out more...
HEA course for new maths lecturers
Last week I had the pleasure of attending a course for new maths
lecturers run by the
Maths, Stats and Operations Research discipline
of the Higher Education Academy (HEA/MSOR). I was pleased that it
dispelled several myths for me, in particular the myth that these
courses never cater for mathematicians' needs. All the talks were
given by experienced mathematics lecturers or people who have spent a
considerable amount of time undertaking educational research specific
to university-level maths. With such good quality input, and with the
high level of engagement discussion amongst the participants, I
learned a lot.
Read on for a couple of ideas I took away (not necessarily
maths-specific!).
Lines through four lines
(Reposting this from an earlier blog which I gave up on, but liked the
post so I added some pictures – all images produced using the amazing
free alternative to Maple/Mathematica, Sage).
I was reading Fulton-Pandharipande ("Notes on stable maps and quantum
cohomology") the other day and came across the classical result that
there are exactly two lines passing through a generic quadruple of
lines in \(\mathbf{CP}^3\). I encourage people to whom this fact is
unfamiliar to convince themselves of it. It was unfamiliar to me and I
found it hard to visualise, so I sat down and drew some pictures until
I understood it.
Read on for more...
Quantum computers: Grover's algorithm
I've been meaning to get my head around the idea of a quantum computer
for a while now and, since my mathematical energy is currently reduced
to clearing out my ETH office, I thought I'd do some reading and find
out more. I leafed through my dusty copy of Wikipedia, picked up
Kitaev et al from the library and turned to chapter two...
I think the easiest way to illustrate how a quantum computer differs
(functionally) from a classical computer is by explaining an algorithm
which only makes sense for quantum computers and which really
outperforms a classical algorithm for the same task (that is the point
of quantum computers, after all). The first algorithm they explain in
Kitaev et al is called Grover's algorithm and it performs the task of
searching a database. Wikipedia has a really nice exposition too, but
I was initially confused by what they both call a "quantum oracle"
(sounds like something from Star Trek TNG). I tried to explicitly
avoid that in what I said below.
TLDR: Classically you have to look through all \(N\) elements
of a database until you find the right one (so runtime increases
linearly in N); Grover's algorithm has a surprising runtime of order
\(\sqrt{N}\) to do the same thing, using clever ideas from quantum
mechanics.
Read on to find out more...



