3-dimensional lightbulb theorem

Recently, Gabai proved a fantastic theorem about knotted surfaces $\Sigma\subset S^2\times S^2$. You can read about it in Gabai's paper, or in Edwards's expository paper. The theorem says that if $\Sigma$ intersects $\{p\}\times S^2$ once transversely then $\Sigma$ is actually unknotted (i.e. it's isotopic to one of the standard spheres $\{(z,z^k)\ :\ z\in\mathbf{C}\cup\{\infty\}\}$). This is the analogue of a (trivial) classical unknottedness theorem in 3 dimensions, called the lightbulb theorem, which I didn't actually know about until I heard about Gabai's result. In this blogpost, I want to discuss the idea behind the 3-dimensional lightbulb theorem (I haven't yet understood the proof of the 4-dimensional version).

3-dimensional lightbulb theorem

The 3-dimensional lightbulb theorem states that any knot $K\subset S^1\times S^2$ which intersects $\{p\}\times S^2$ once transversely is unknotted (isotopic to $S^1\times\{q\}$ for some $q\in S^2$). When I heard this statement, my immediate reaction was: surely that's wrong?! You can always knot things locally in a small ball without changing the intersection with $\{p\}\times S^2$; why should you suddenly be able to undo those knots? However, you can quickly draw yourself a picture to convince yourself that it's true.

Unknotting knotted rays

Here's one way to visualise $S^1\times S^2$: take the "solid annular" region between two concentric spheres (say at radii 1 and 2) in 3-space, and identify the two spheres (i.e. whenever you move across the sphere at radius 1 you reappear at the point in the sphere at radius 2 which lies on the same ray through the origin, and vice versa). In this picture, the circles $S^1\times\{q\}$ are precisely the segments of rays through the origin which intersect the solid annulus (shown in red below; $q$ specifies which ray).

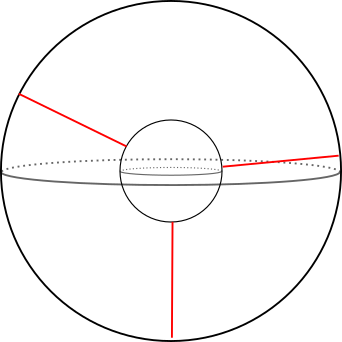
The kind of knots that the classical lightbulb theorem talks about are the following. Take a ray segment, cut out the middle bit, and replace it with a knotted arc in the interior of the solid annulus (with the same endpoints). I'll call this a "knotted ray".

Why should you be able to unknot this?

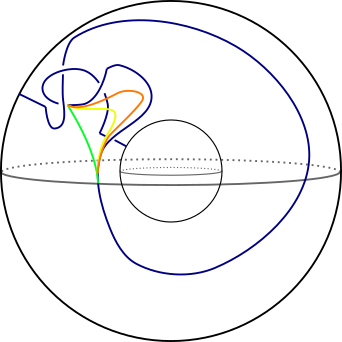
Well, in this picture it's not too hard to see why. You can try to change a crossing by isotoping one of the strands around the back of the inner sphere. Here's a sequence of pictures which illustrates what I mean (red knots are snapshots of the isotopy, the colourful pictures are supposed to indicate an isotopy in progress). We change the rightmost crossing from an over- to an under-crossing. As soon as you can change crossings like this, you can unknot things very easily.

What about the knot group?

Usually, codimension 2 knotting is related to the knot complement having nontrivial fundamental group. For a loop $S^1\times\{q\}$, the complement is $S^1\times(S^2\setminus\{q\})$, which is homotopy equivalent to $S^1$. The usual generator for the knot group (the meridian which links the knot) is nullhomotopic. The same is true for any knotted ray: if we take the sphere $\{p\}\times S^2$ which our knotted ray intersects once transversely then we can take a meridian for the knotted ray which sits in this sphere; this meridian then bounds a disc in this sphere.

Why "lightbulb"?

You're supposed to think of the inner sphere as a lightbulb, connected to the outer sphere (ceiling) by a cord (knotted ray). This intuition makes it absolutely clear why you can unknot: you just push the bulb back along the cord until all the knots come undone; then you say that that this is equivalent to doing an isotopy of the cord and keeping the bulb fixed.