Focus-focus singularities

I am currently giving a graduate-level lecture course on Lagrangian torus fibrations. One of the side-products of this is some images which I have generated using a computer and which I want to display in class. The lectures are being held outside of the university, so it costs extra to hire a projector, and I am not using a projector for the majority of the lectures, so instead I will post these images to this blog and direct students to look at them using their mobile devices (or the mobile device of their neighbour, if they don't have one).

The images illustrate the developing map for the integral affine structure on the base of a Lagrangian torus fibration in the neighbourhood of a focus-focus fibre.

More precisely, the map in question goes from \(\tilde{B}\), the universal cover of the punctured plane, to \(\mathbf{R}^2\). If we use coordinates \(re^{i\theta}\), \(r>0\) on the punctured plane (so that \(\theta\) lifts to a well-defined function on the universal cover) then the map is \[I(r,\theta)=(r\theta\sin\theta-r\cos\theta(\log r-1),r\cos\theta).\] It was proved by San Vu Ngoc that this is the map which, when restricted to any fundamental domain in \(\tilde{B}\) for the action of the deck group, gives action coordinates for a particular integrable Hamiltonian system with a focus-focus singularity. The images of different fundamental domains are related by an integral affine transformation called the affine monodromy (in this case, just the matrix \(\begin{pmatrix}1&1\\0&1\end{pmatrix}\)). For more information, read my lecture notes for the course (Chapter 3 is where the pictures appear).

Without further ado, here are the images. The red lines are the images of radii, the blue lines are the images of contours with fixed radius.

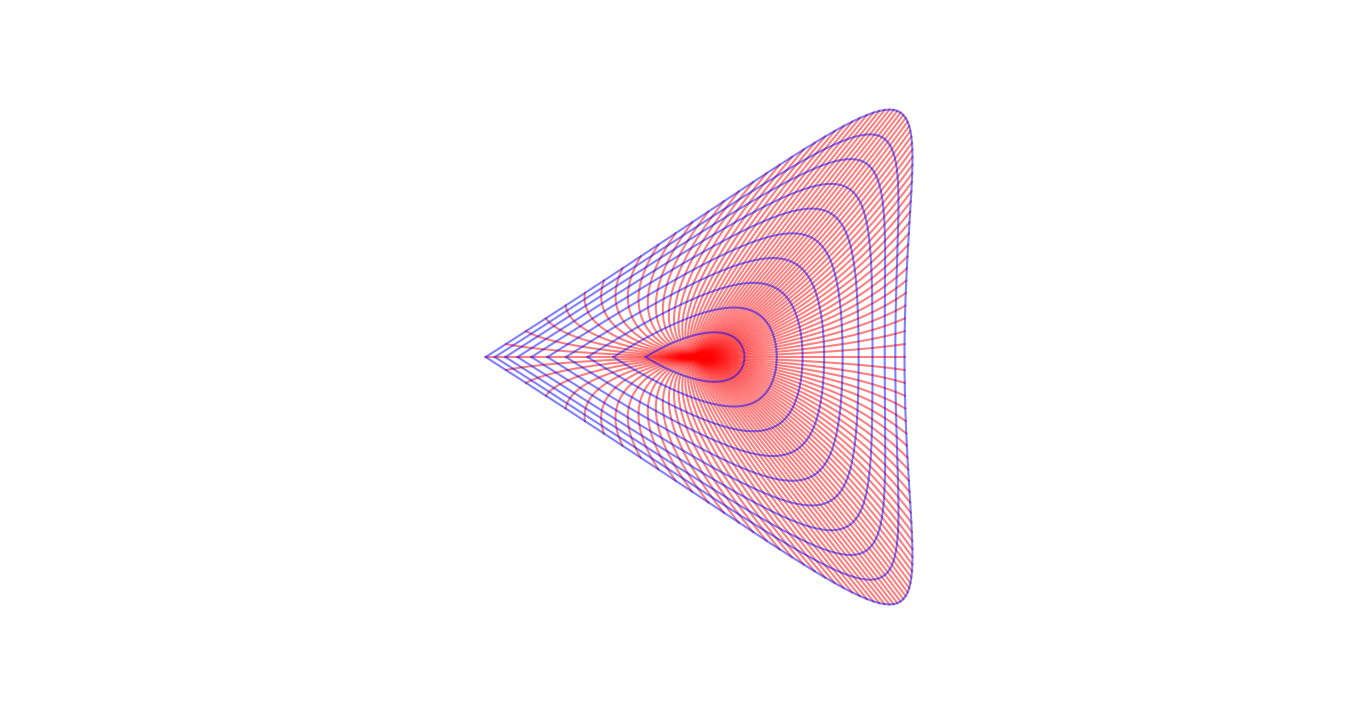
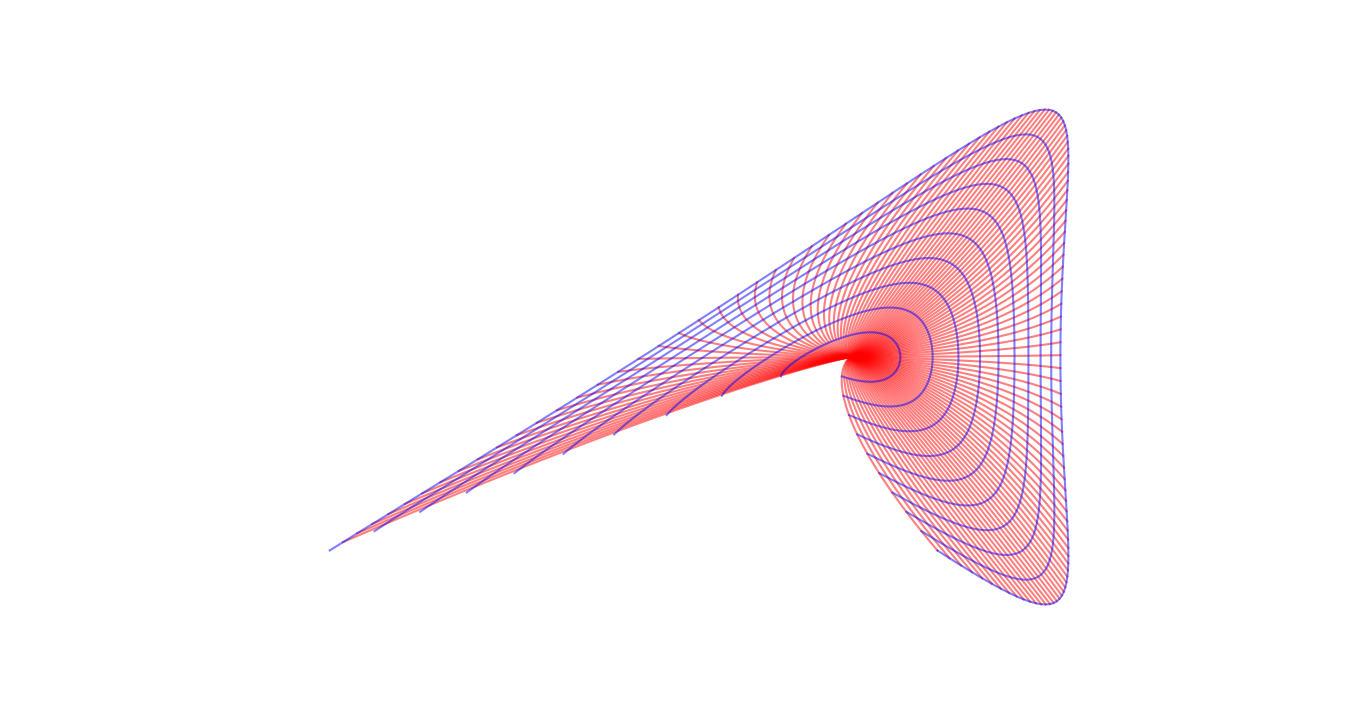
In left-hand figure, we see the the image of the fundamental domain \(\{\theta\in[-\pi,\pi)\}\), in the right the image of the fundamental domain \(\{\theta\in[-5\pi/7,9\pi/7)\}\). The fact that the plot on the right does not ``close up'' is because of the monodromy: the image of the radius \(\theta=-5\pi/7\) and the image of the radius \(\theta=9\pi/7\) are related by the monodromy matrix. The fact that the first plot does ``close up'' is because the line \(\theta=\pi\) is an eigendirection for the monodromy matrix.

In the third figure, we see the image of two fundamental domains \(\{\theta\in[-5\pi/2,3\pi/2)\}\), related to one another by the action of the monodromy matrix. Anyone who has compulsively traced out the spiral of a raffia mat cannot fail to be moved by this image.