Small resolutions
I was discussing all of this with my collaborator Mirko Mauri and trying to understand when small resolutions exist in more complicated situations. He told me something which blew my mind. "Small resolutions often occur when you blow up a divisor." Don't be silly, I said, blowing up a divisor doesn't do anything. He pointed out that blowing up a Cartier divisor doesn't do anything, but blowing up a Weil (but non-Cartier) divisor can do something. At this point, I was trying to remember what the difference was and whether all Cartier divisors were Weil or vice versa or neither. By the end of our discussion, I had a much better understanding of what "blowing up a divisor" means from the viewpoint of a symplectic geometer. I try to explain this below.
A Weil divisor \(D\) is the thing which corresponds to the idea of divisor in my head: a bunch of subschemes with weights attached. This is the thing that gives you a coherent sheaf \(\mathcal{O}(D)\) whose sections are rational functions having poles of order at most (weight) along \(D\) (or having zeros of order at least (-weight)).
A Weil divisor is Cartier if this sheaf is the sheaf of sections of a line bundle. If \(X\) is not too singular (normal) then a Weil divisor is Cartier if it is everywhere locally cut out by a single equation.
Let's look at the example of the 3-fold ordinary double point. This is the affine variety \(X=\{(x,y,z,w)\in\mathbf{C}^4\ :\ xy=zw\}\), which has an isolated singularity at the origin.
If we look at the divisor \(x=0\) (which is cut out by one equation, hence Cartier) then we get a reducible subvariety (because \(x=0\) implies \(zw=0\), so either \(z=0\) or \(w=0\), hence we have two components). Similarly \(y=0\) has two components. These four components are Weil but not Cartier: you need two equations (like \(x=z=0\)) to cut them out.
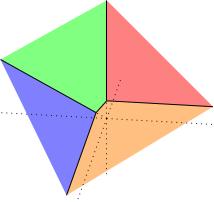
There is a nice picture of the 3-fold ODP because it's toric: the three circle actions \((x,y,z,w)\mapsto (e^{i\theta} x,y,e^{i\theta}z,w)\), \((x,y,z,w)\mapsto (e^{-i\theta} x,e^{i\theta}y,z,w)\), \((x,y,z,w)\mapsto (e^{i\theta} x,y,z,e^{i\theta}w)\) commute and preserve the variety. The moment maps for these circle actions are \(\mu_1=\frac{1}{2}(|x|^2+|z|^2)\), \(\mu_2=\frac{1}{2}(|y|^2-|x|^2)\) and \(\mu_3=\frac{1}{2}(|x|^2+|w|^2)\). The image of the variety under \((\mu_1,\mu_2,\mu_3)\colon X\to\mathbf{R}^3\) is a cone spanned by the four rays in the positive \((1,-1,1)\)-, \((1,0,0)\)-, \((0,1,0)\)- and \((0,0,1)\)-directions (these rays are the projections of the curves \(y=z=w=0\), \(x=y=w=0\), \(x=z=w=0\) and \(x=y=z=0\) respectively).
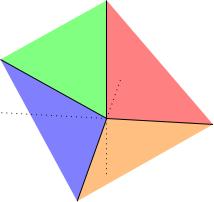
The four Weil-but-not-Cartier divisors \(x=z=0\), \(x=w=0\), \(y=z=0\), \(y=w=0\) project to the four faces of this cone. Let's pick one of them, say \(x=w=0\) (which projects to the horizontal face). What does it mean to "blow-up" this divisor? In symplectic geometry, blowing up a divisor means you cut out a neighbourhood of the divisor, observe that the boundary of the neighbourhood has a characteristic foliation whose leaves are closed circles, and collapse these circles down to points. In the toric picture, the neighbourhood of this divisor is just the set of points with \(\mu_3<\epsilon\) for some \(\epsilon\). When you cut it out and collapse the characteristic foliation ("symplectic cut") you get another toric variety whose moment polytope is obtained by discarding everything below \(\mu_3=\epsilon\). If you look at this polytope, you get exactly the polytope for the small resolution.