08. Other operations
08. Other operations
Matrix addition
In this video, we'll define some further operations you can do to produce new matrices. The first is matrix addition If we have two m-by-n matrices A and B with entries A_{i j} and B_{i j}, we can form a new matrix A + B with (A + B)_{i j} = A_{i j} + B_{i j}. In other words, you take the i jth entries of both matrices and add them.
the 2-by-2 matrix 1, 0; 1, 1 plus the 2-by-2 matrix 1, 1; 0, minus 1 equals the 2-by-2 matrix 2, 1; 1, 0.
Special case: vector addition
This is most useful when A and B are both column vectors, i.e. m-by-1 matrices. Let's see what it means in for vectors in R 2. The formula is x, y plus a, b equals x + a, y + b
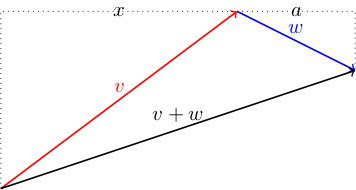
Geometrically, we add two vectors v = x, y and w = a, b by translating w to the tip of v and drawing the arrow from the tail of v to the tip of w. One can see from the picture that the x- (respectively y-) coordinate of this arrow is the sum of the x- (respectively y-) coordinates of v and w.
Rescaling
Given a number lambda and a matrix A, you can form the matrix \lambda A whose entries are lambda times the entries of A.
2 times the 2-by-2 matrix 1, 2; 3, 4 equals the 2-by-2 matrix 2, 4; 6, 8.
Matrix exponentiation
The exponential of a number x is defined by the Taylor series of exp: exp of x equals 1 plus x plus x squared over 2 factorial plus x cubed over 3 factorial plus dot dot dot, which equals the sum over n from 0 to infinity of x to the n over n factorial. We can use the same definition to define the exponential of a matrix: exp of M equals the sum over n from 0 to infinity of M to the n over n factorial. Here, A to the zero is understood to mean the identity matrix I (the analogue for matrices of the number 1).
Consider M, the 2-by-2 matrix 0, 1; 0, 0. Since M squared equals zero, all the higher powers of M vanish (the name for this is nilpotence: some power of M is zero), so the matrix exponential becomes exp of M equals I plus M, which equals 1, 1; 0, 1. So we get the matrix for a shear as the exponential of a nilpotent matrix.
In fact, exp of 0, t; 0, 0 equals 1, t; 0, 1, so we get a whole family of matrices which shear further and further to the right as t varies.
Take M to be the 2-by-2 matrix 0, minus t; t, 0. We have M equals t times 0, minus 1; 1, 0, M squared equals minus t^2, 0; 0, minus t squared, which equals minus t squared times the identity, M cubed equals minus t cubed times 0, minus 1; 1, 0, M to the four equals minus t to the four times the identity etc.
and in the end we get exp of M equals the identity plus t times 0, minus 1; 1, 0, minus t squared over 2 times the identity, minus t cubed over 3 factorial times 0, minus 1; 1, 0, plus t to the 4 over 4 factorial times the identity, plus t to the 5 over 5 factorial times 0, minus 1; 1, 0, etc. The coefficient of I is the Taylor series for cos t; the coefficent of 0, minus 1; 1, 0 is the Taylor series for sine t, so overall we get exp of M equals cos t, minus sine t; sine t, cos t. So we get a general rotation matrix in 2-d by exponentiating this very simple matrix.