09. Dot product, 1

Dot product

Given two vectors $v=\begin{pmatrix}v_{1}\\ \vdots\\ v_{n}\end{pmatrix}$ and $w=\begin{pmatrix}w_{1}\\ \vdots\\ w_{n}\end{pmatrix}$ in $\mathbf{R}^{n}$ , what is the angle between them?

0.43 To define angles in $\mathbf{R}^{n}$ , note that the two vectors $v$ and $w$ are contained in a unique 2-plane, and we mean the usual angle between $v$ and $w$ inside that plane.

1.45 To compute that angle, we introduce the dot product $v\cdot w$ .

Definition:

The dot product $v\cdot w$ is the number $v_{1}w_{1}+\cdots+v_{n}w_{n}$ .

Theorem:

2.50 If $\theta$ is the angle between $v$ and $w$ then $v\cdot w=|v||w|\cos\theta.$ Recall that $|v|$ means the length of $v$ .

We will prove this in due course, but first we'll explore it a little.

3.47 Let $v=\begin{pmatrix}1\\ 0\end{pmatrix}$ and $w=\begin{pmatrix}0\\ 1\end{pmatrix}$ . We have $v\cdot w=1\times 0+0\times 1=0$ .

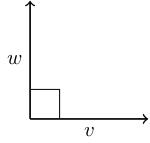
The vectors v=(1,0) and w=(0,1) (at right angles)

4.38 This makes sense: the angle between $v$ and $w$ is $\pi/2$ radians, and $\cos(\pi/2)=0$ . In this case, we say the vectors are orthogonal to one another (equivalent to "perpendicular" or "at right angles").

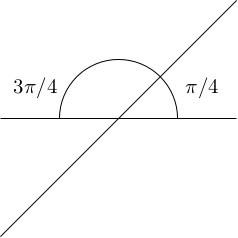
5.32 Let $v=\begin{pmatrix}1\\ 1\end{pmatrix}$ and $w=\begin{pmatrix}1\\ 0\end{pmatrix}$ . We can see the angle between them should be 45 degrees ( $\pi/4$ radians).

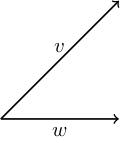
The vectors v=(1,1) and w=(1,0) (at 45 degrees)

Let's confirm this: we have $v\cdot w=1\times 1+0\times 1=1$ . We also have $|v|=\sqrt{1+1}=\sqrt{2}$ by Pythagoras and $|w|=1$ , so $1=v\cdot w=|v||w|\cos\theta=\sqrt{2}\cos\theta,$ so $\cos\theta$ should be $1/\sqrt{2}$ . Indeed, $\cos(\pi/4)=1/\sqrt{2}$ .

8.12 Even if you didn't know the angle, you could figure it out as $\arccos(1/\sqrt{2})$ . You might object that $\arccos$ is multivalued, for example $\cos(\pi/4)=\cos(3\pi/4)$ . This just corresponds to the fact that there are different ways of picking "the" angle between $v$ and $w$ (e.g. clockwise or anticlockwise).

Two lines which meet at 45 degrees could also be thought of as meeting at 135 degrees