An n-by-n matrix M is orthogonal if M transpose times M equals the identity.
11. Dot product, 3
11. Dot product, 3
Orthogonal matrices
This is equivalent to saying that:
-
the columns of M, considered as column vectors, are orthogonal to one another, and
-
each column has length one when considered as a vector.
The matrix M equals cos theta, minus sine theta; sine theta, cos theta is orthogonal: M transpose M equals cos theta, sine theta; minus sine theta, cos theta times cos theta, minus sine theta; sine theta, cos theta; which equals cos squared theta plus sine squared theta, minus sine theta cos theta plus cos theta sine theta; sine theta cos theta minus cos theta sine theta, cos squared theta plus sine squared theta, which equals 1, 0; 0, 1.
If M is orthogonal then the geometric transformation of R n defined by M preserves dot products, i.e. M v dot M w equals v dot w.
M v dot M w equals v transpose M transpose M w, which equals v transpose times the identity times w, which equals v transpose w, which equals v dot w.
In particular, orthogonal matrices preserve lengths of vectors. This is because norm v equals square root of v_1 squared plus dot dot dot plus v_n squared, which equals the square root of v dot v and orthogonal matrices preserve dot products.
The sorts of transformations you should have in mind when you think of orthogonal matrices are rotations, reflections and combinations of rotations and reflections.
We now turn to the proof of the formula v dot w equals norm v norm w cos theta where theta is the angle between v and w.
The "proof" I'll give is more of an intuitive argument. I'll point out where the dodgy bits are as we go on.
The angle between v and w is defined by taking the plane spanned by v and w and taking the angle between them inside that plane. Therefore without loss of generality, we can assume v and w are in the standard R 2. ( This is where the dodgy bit is: technically, we need to check that the plane spanned by v and w is the same, geometrically (isometric to) the standard R 2; this would require us to appeal to something like Gram-Schmidt orthogonalisation, which you'll see in a later course on linear algebra.)
Further, we can rotate using our 2-by-2 rotation matrix so that v points in the positive x-direction. We can do this without changing the angle theta (because rotations preserve angles) and without changing the dot product (because rotations are orthogonal, so don't change dot products).
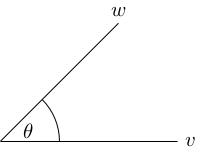
Finally, compute v dot w equals v_1 w_1 plus v_2 w_2, which equals v_1 w_1 because v_2 = 0. We have v_1 equals norm v because v points along the positive x-axis. We also have w_1 equals norm w times cos theta. So overall we have v dot w equals norm v norm w cos theta.
If you were disturbed by my claim that rotations preserve angles without justification, you should have been even more disturbed by the fact that I didn't actually define angles in the plane at all. This is not intended as a complete rigorous derivation from axioms, but as an appeal to your geometric intuition.