11. Dot product, 3

Orthogonal matrices

Definition:

0.33 An $n$ -by- $n$ matrix $M$ is orthogonal if $M^{T}M=I$ .

This is equivalent to saying that:

the columns of $M$ , considered as column vectors, are orthogonal to one another, and
each column has length one when considered as a vector.

Example:

2.24 The matrix $M=\begin{pmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}$ is orthogonal: $M^{T}M=\begin{pmatrix}\cos\theta&\sin\theta\\ -\sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}=\begin{pmatrix}\cos^{2}\theta+\sin^{2}% \theta&-\sin\theta\cos\theta+\cos\theta\sin\theta\\ \sin\theta\cos\theta-\cos\theta\sin\theta&\cos^{2}\theta+\sin^{2}\theta\end{% pmatrix}=\begin{pmatrix}1&0\\ 0&1\end{pmatrix}=I.$

Lemma:

5.48 If $M$ is orthogonal then the geometric transformation of $\mathbf{R}^{n}$ defined by $M$ preserves dot products, i.e. $(Mv)\cdot(Mw)=v\cdot w$ .

$(Mv)\cdot(Mw)=v^{T}M^{T}Mw=v^{T}Iw=v^{T}w=v\cdot w.$

7.50 In particular, orthogonal matrices preserve lengths of vectors. This is because $|v|=\sqrt{v_{1}^{2}+\cdots+v_{n}^{2}}=\sqrt{v\cdot v}$ and orthogonal matrices preserve dot products.

8.50 The sorts of transformations you should have in mind when you think of orthogonal matrices are rotations, reflections and combinations of rotations and reflections.

9.29 We now turn to the proof of the formula $v\cdot w=|v||w|\cos\theta$ where $\theta$ is the angle between $v$ and $w$ .

The "proof" I'll give is more of an intuitive argument. I'll point out where the dodgy bits are as we go on.

10.26 The angle between $v$ and $w$ is defined by taking the plane spanned by $v$ and $w$ and taking the angle between them inside that plane. Therefore without loss of generality, we can assume $v$ and $w$ are in the standard $\mathbf{R}^{2}$ . (11.10 This is where the dodgy bit is: technically, we need to check that the plane spanned by $v$ and $w$ is the same, geometrically (isometric to) the standard $\mathbf{R}^{2}$ ; this would require us to appeal to something like Gram-Schmidt orthogonalisation, which you'll see in a later course on linear algebra.)

12.17 Further, we can rotate using our 2-by-2 rotation matrix so that $v$ points in the positive $x$ -direction. We can do this without changing the angle $\theta$ (because rotations preserve angles) and without changing the dot product (because rotations are orthogonal, so don't change dot products).

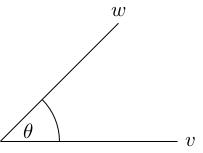
Vectors v (horizontal) and w (at an angle theta)

13.36 Finally, compute $v\cdot w=v_{1}w_{1}+v_{2}w_{2}=v_{1}w_{1}$ because $v_{2}=0$ . We have $v_{1}=|v|$ because $v$ points along the positive $x$ -axis. We also have $w_{1}=|w|\cos\theta$ . So overall we have $v\cdot w=|v||w|\cos\theta$ .

14.30 If you were disturbed by my claim that rotations preserve angles without justification, you should have been even more disturbed by the fact that I didn't actually define angles in the plane at all. This is not intended as a complete rigorous derivation from axioms, but as an appeal to your geometric intuition.