12. Rotations

Example 1

0.25 Let . This is an example of a 3-by-3 rotation matrix. The top-left 2-by-2 block rotates the $xy$ -plane, and the 1 in the bottom-right tells us that the $z$ -axis is fixed. More precisely: so the vectors $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill 0\hfill \end{array}\right)$ in the $xy$ -plane get rotated by the 2-by-2 rotation matrix , and the vector $\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right)$ which points along the $z$ -axis is fixed.

2.33 A key point here is that the axis of rotation is fixed, i.e. any vector $u$ pointing in the $z$ -direction satisfies $u=Au$ .

Example 2

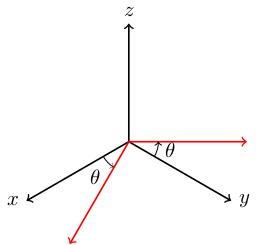
3.26 Let . This is another example of a 3-by-3 rotation matrix. What is the axis of rotation? We need to find a vector $u=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$ such that $u=Bu$ . In other words, 4.50 This is three equations (one for each component): $$x=z,y=y,-x=z.$$ The equation $y=y$ is trivially satisfied. The other two equations imply $x=z=0$ . Therefore $u=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill y\hfill \\ \hfill 0\hfill \end{array}\right)$ , and $u$ must point along the $y$ -axis.

5.47 By comparing with Example 1, the angle of rotation can be found by:

• taking a vector $v$ which lives in the plane orthogonal to the axis,

• applying $B$ to get $Bv$ ,

• computing the angle between $v$ and $Bv$ using dot products.

6.15 For example, we could take $v=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$ (as $v\cdot u=0$ so $v$ is orthogonal to the axis). Then $Bv=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -1\hfill \end{array}\right)$ , so $v\cdot Bv=0$ . If $\theta$ is the angle between $v$ and $Bv$ then this implies $\cos \theta =0$ , so $\theta =\pm 90$ degrees.

8.35 In fact, we can understand exactly what this rotation is doing by drawing the images of the basis vectors $e_1,e_2,e_3$ under $B$ (i.e. the three columns of $B$ ). The vector $e_2$ is fixed, $e_3$ goes to $e_1$ and $e_1$ goes to $-e_3$ , so this rotates by 90 degrees about the $y$ -axis, sending the positive $z$ -axis to the positive $x$ -axis.

Example 3

9.50 Take . This is another 3-by-3 rotation matrix; we'll find the axis and angle of rotation.

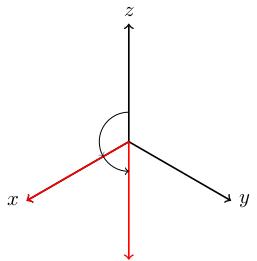
10.36 To find the axis $u=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)$ , we need to solve $u=Cu$ : The first two equations imply $x=y=z$ , so the third is redundant, and any vector of the form $u=\left(\begin{array}{c}\hfill x\hfill \\ \hfill x\hfill \\ \hfill x\hfill \end{array}\right)$ is fixed. In other words, the axis points in the $\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)$ -direction.

12.12 To find the angle, pick a vector $v$ orthogonal to $u$ . For example, $v=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \end{array}\right)$ satisfies $u\cdot v=0$ so is orthogonal to $u$ . We compute $$v\cdot Cv=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \\ \hfill 0\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill -1\hfill \end{array}\right)=-1.$$ We also know that if $\theta$ is the angle between $v$ and $Cv$ then $-1=v\cdot Cv=|v||Cv|\cos \theta$ . Since $|v|=|Cv|=\sqrt{2}$ , we get $$\cos \theta =-1/2.$$ This tells us that $\theta$ is $2\pi /3$ (or any of the other values that have $\cos \theta =-1/2$ ). Let's draw a picture to convince ourselves it's really $2\pi /3$ (120 degrees).

14.56 The axis of rotation points out of the screen: