17. Geometric viewpoint on simultaneous equations, 1

0.00 In this video and the next, we'll develop a geometric point of view on simultaneous equations.

2 variables

0.20 We've repeatedly studied the system of equations $x-y=-1,\qquad x+y=3.$ We saw this has the unique solution $x=1$ , $y=2$ . Geometrically, $x-y=-1$ and $x+y=3$ define lines in the $x y$ -plane: the first (red) is $y=x+1$ (slope $1$ , $y$ -intercept $1$ ), the second (blue) is $y=-x+3$ (slope $-1$ , $y$ -intercept $3$ ):

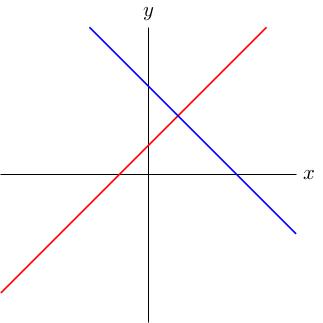
Red line with slope 1 and y-intercept 1 intersects blue line with slope -1 and y-intercept 3 at (1,2)

2.30 They intersect at exactly one point, namely $(1,2)$ . This is precisely the solution of the equations ( $x=1$ , $y=2$ ). That makes sense: the first line is the set of points whose $x$ and $y$ coordinates satisfy $x-y=-1$ , the second line is the set of points whose coordinates satisfy $x+y=3$ ; the intersection is the set of points whose coordinates satisfy both equations.

So solving simultaneous linear equations in two variables is the same thing as intersecting lines.

3.43 Let's add another equation: $x-y=-1,\qquad x+y=3,\qquad 2x-y=0.$ This adds another line (orange) into our diagram.

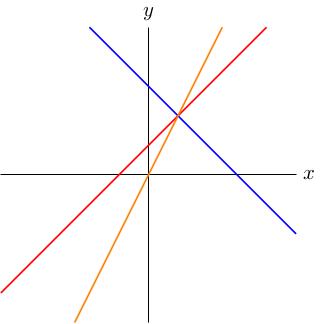
Three lines which meet at one triple point

Since these lines have a common triple intersection point $(1,2)$ , this is still a solution to this system of equations.

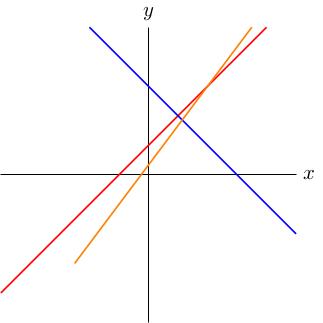
5.10 If we had picked a slightly third different equation, defining a line which didn't pass through $(1,2)$ , there would be no solutions. For example: $x-y=-1,\qquad x+y=3,\qquad 2x-y=1,$ defines three lines which have no triple intersection point, so there is no common solution.

Three lines which fail to meet at one triple point

Lines in the plane

6.54 Each equation $a_{1}x+a_{2}y=b$ defines a line in the plane. A solution of the system of equations is a common intersection point between these lines.

The line $L=\{(x,y)\in\mathbf{R}^{2}\ :\ a_{1}x+a_{2}y=b\}$ is equivalent to $y=-\frac{a_{1}}{a_{2}}x+\frac{b}{a_{2}}$ (if $a_{2}\neq 0$ , otherwise it's vertical), so the slope is $-a_{1}/a_{2}$ (infinity if $a_{2}=0$ ).

Lemma:

7.57 The vector $\begin{pmatrix}a_{1}\\ a_{2}\end{pmatrix}$ is orthogonal to $L$ . (It's also called the "normal vector to $L$ ").

If I pick two points $\begin{pmatrix}x\\ y\end{pmatrix}$ and $\begin{pmatrix}x^{\prime}\\ y^{\prime}\end{pmatrix}$ on $L$ then their difference $\begin{pmatrix}x-x^{\prime}\\ y-y^{\prime}\end{pmatrix}$ points along $L$ , so it's sufficient to check that $\begin{pmatrix}a_{1}\\ a_{2}\end{pmatrix}\cdot\begin{pmatrix}x-x^{\prime}\\ y-y^{\prime}\end{pmatrix}=0.$ 9.29 We have $\begin{pmatrix}a_{1}\\ a_{2}\end{pmatrix}\cdot\begin{pmatrix}x-x^{\prime}\\ y-y^{\prime}\end{pmatrix}=a_{1}x+a_{2}y-a_{1}x^{\prime}-a_{2}y^{\prime}=b-b=0$ , since $a_{1}x+a_{2}y=a_{1}x^{\prime}+a_{2}y^{\prime}=b$ (both points lie on $L$ ).