More generally, the dimension of the subspace of solutions equals the number of free variables: we can think of the free variables as parameters for describing points in the subspace of solutions.
18. Geometric viewpoint on simultaneous equations, 2
18. Geometric viewpoint on simultaneous equations, 2
3 variables
Now let's look at higher dimensional systems.
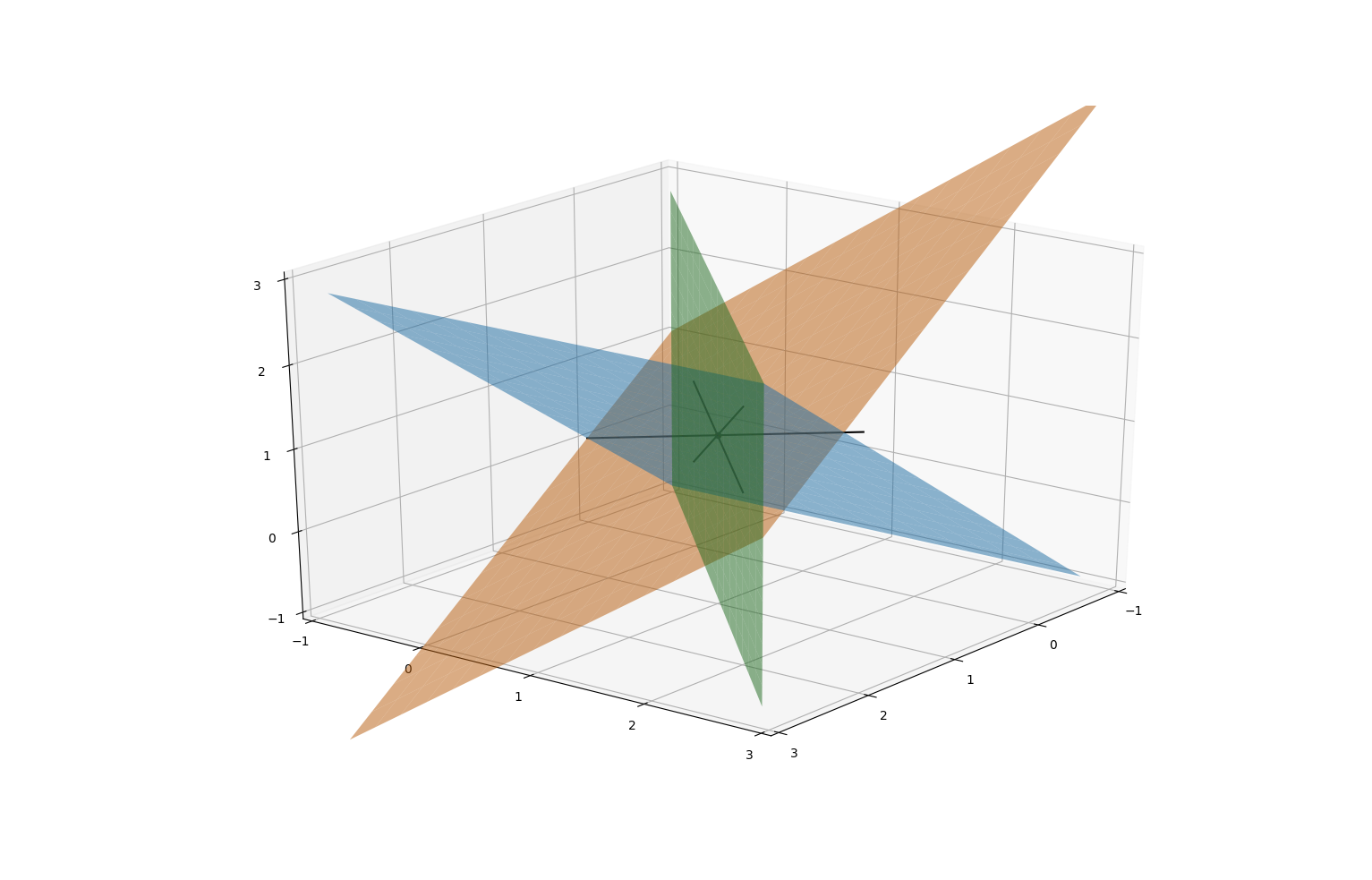
Consider the equations x minus y + z equals 1, x minus z = 0. The set of points whose coordinates satisfy these equations is a subset of 3-dimensional space R^3. Each equation cuts out a plane; their intersection (the set of simultaneous solutions) is a line. :

The solution of the equations is z = x, y = 2 x minus 1 (x is a free variable); this gives us a parametrisation of the line of intersection: it consists of vectors of the form x, 2 x minus 1, x.
Each equation a_1 x + a_2 y + a_3 z = b gives us a plane. This plane is orthogonal to the vector a_1, a_2, a_3. The z-intercept is where x = y = 0, so z equals b over a_3.
Let's consider the system x minus y + z = 1, x minus z = 0, x minus y = 0. The first two planes are the same as before; the third equation gives a third plane. The set of solutions is the set of triple intersections between these planes. Solving, we get x = y = z and z = y = 2 z minus 1, so x = y = z = 1. Therefore there is a unique triple intersection point at (1, 1, 1).
Higher dimensions
An equation a_1 x_1 + dot dot dot + a_n x_n = b in n variables defines a hyperplane in n-dimensional space R^n. This is the hyperplane orthogonal to the vector a_1, dot dot dot, a_n.
If v = x_1, dot dot dot, x_n is a vector of variables and A v = b is a system of m simultaneous equations encoded with an m-by-n matrix A then each row of A defines a hyperplane A_{i 1} x_1 + dot dot dot + A_{i n} x_n = b_i in R^n. The set of solutions is a subspace of R^n. Subspace is a catch-all name, which includes points, lines, planes, hyperplanes, and everything in between (for which we don't have everyday words).
Consider the equations w + x + y + z = 0 and x minus y = 1. This is a pair of equations in four variables, so defines a subspace of solutions in R^4. Each equation gives a 3-dimensional hyperplane in R^4. Their intersection is a 2-dimensional subspace (plane) living in R^4. Solving the equations: w = minus 2 y minus z, x = 1 minus y. We see that y, z are free variables and w, x are dependent variables. The fact that there are two free variables is another way of saying that the subspace of solutions is 2-dimensional: each free variable is a coordinate on the subspace of solutions.