Theorem:
Let A = a, b; c, d be a 2-by-2 matrix and S inside R^2 be the unit square:
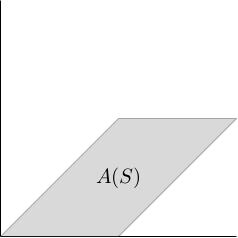
Let A(S) be the image of S under the geometric transformation A (A(S) is a parallelogram. Then the absolute value of det A equals the area of A(S)
29. Geometry of determinants, 1
29. Geometry of determinants, 1
In this video, we will reconnect with geometry.
Example:
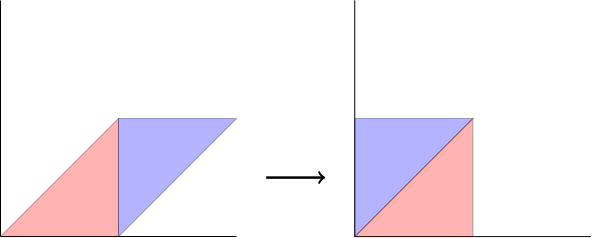
If A = 1, 1; 0, 1 then A(S) looks like this (parallelogram with vertices at (0, 0), (1, 0), (2, 1), (1, 1)):
We can find the area of this parallelogram by decomposing it into two triangles, slicing it vertically between (1, 0) and (1, 1), and then shifting the right-hand triangle to the left until they form a rectangle (actually a square) with side lengths 1 and 1. Since this rearrangement didn't change the area, we see that the area of A(S) is 1, which is indeed the determinant of A.
Proof of theorem
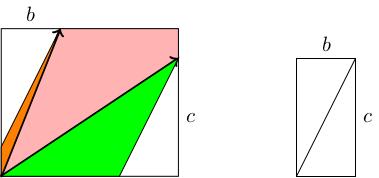
Take the parallelogram A(S) with edges A times 1, 0 = a, c and A times 0, 1 = b, d. We will draw a rectangle with its bottom-left corner at the origin, height d and base a. This passes through the vertices a, c and b, d.
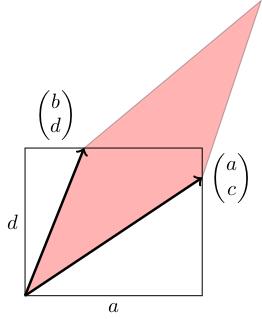
The area of this rectangle is a d. Let's subdivide A(S) into pieces, rearrange them so they live inside this rectangle, and observe that there's still a bit missing, which has area b c, which will prove that area of A(S) equals a d minus b c.
We draw a line connecting the top right corner of the rectangle to the top right corner of the parallelogram. Together with the rectangle, this cuts our parallelogram into three pieces. We shift the parts outside the rectangle until they sit inside the rectangle, and so that the edges which used to be opposite parallel edges match up:
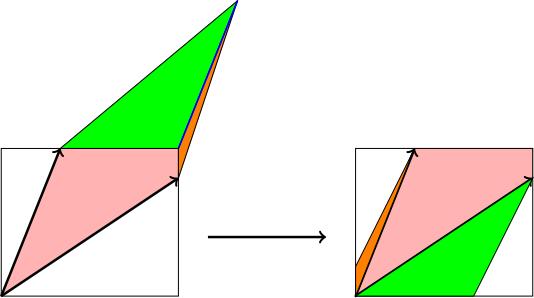
What's missing? There are two (white) triangles still missing. These triangles share a parallel edge, so can be rearranged to form a rectangle. They have base b and height c, so the total missing area is b c. Therefore the area of A(S) equals the area of the big rectangle (a d) minus the total area of these two triangles (b c).
