If A is an n-by-n matrix and S insideR^n is the unit n-dimensional cube then the absolute value of det A equals the volume of A(S).
30. Geometry of determinants, 2
30. Geometry of determinants, 2
Higher dimensions
Last time we saw a geometric interpretation of the determinant of a 2-by-2 matrix A as the area of a parallelogram obtained by applying A to a square. This result holds in all dimensions, though we will not prove it:
The absolute value signs around the determinant need to be there because areas and volumes are positive but determinants can be negative. In the proof of the 2-by-2 case, I hid the issue in the picture I drew: if I had switched the vectors a, c and b, d in the picture, we would have ended up with b c minus a d, i.e. minus det A.
In higher dimensions, A(S) is no longer a parallelogram, but a parallelopiped ("parallel-legged"): a shape whose faces are parallel pairs of congruent parallelograms.
Tetrahedra/simplices
Another useful characterisation of the determinant (which we won't prove) is the following.
Let a_1, a_2, etc up to a_n be vectors in R^n. Consider the simplex with vertices at 0, a_1, a_2, etc up to a_n. Then the volume of this simplex is det A over n factorial where A is the matrix with columns a_1 up to a_n.
A simplex is the simplest convex shape you can draw with these vertices: you take the vertices, connect them by lines, and then fill in all the space in between. (More formally, this is called taking the convex hull of the vertices). In 2 dimensions this gives a triangle (3 vertices). In 3 dimensions you get a tetrahedron.
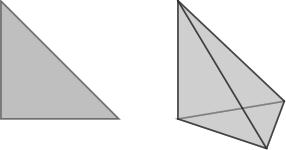
These two theorems are closely related: you can decompose a cube into n factorial simplices. Rather than proving either of them, I want to use this second theorem to calculate the volumes of some tetrahedra in R^3.
Take a_1 = 1, 0, 0, a_2 = 0, 1, 0 and a_3 = 0, 0, 1. The corresponding tetrahedron has volume 1 over 6 times det of the identity matrix, which equals 1 over 6.
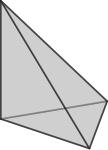
Take a regular tetrahedron (d4 for the roleplayers out there) with vertices at a_0 = 1, 1, 1, a_1 = 1, minus 1, minus 1, a_2 = minus 1, 1, minus 1 and a_3 = minus 1, minus 1, 1. (These vertices are half of the vertices of a regular cube centred at the origin with sidelength 2.)
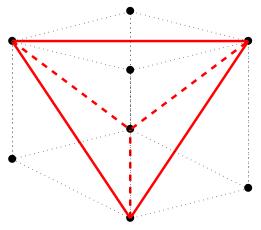
Translating by minus a_0, we get the vertices 0, a_1 minus a_0, a_2 minus a_0, a_3 minus a_0, so we can apply our theorem with A the 3-by-3 matrix with columns a_1 minus a_0, a_2 minus a_0 and a_3 minus a_3, i.e. 0, minus 2, minus 2; minus 2, 0, minus 2; minus 2, minus 2, 0. We compute the determinant using the cofactor expansion along the top row: volume equals the absolute value of 1 over 6 time det of this matrix, which equals 1 over 6 times the absolute value of minus minus 2 times det of minus 2, minus 2; minus 2, 0; minus twice the determinant of minus 2, 0, minus 2, minus 2 which equals 2 over 6 times the absolute value of minus 4 minus 4 which equals 16 over 6
Determinant as scale factor for volumes
det A is the scale factor for volumes of cubes under the transformation A. Since any volume is defined by subdividing/approximating by smaller and smaller cubes, det A is the scale factor for any volume under the transformation A. From this point of view, the formula det of the product A B equals det A times det B is just telling us that if we apply the transformation B and then the transformation A, the volumes rescale by det B and then by det A, giving a total scale factor of det A times det B for the composite transformation.