If v is an eigenvector of A with eigenvalue lambda ("a lambda-eigenvector") then so is k v for any k in C.
34. Eigenspaces
34. Eigenspaces
In all the examples we've seen so far, the eigenvectors have all had a free variable in them. For example, in the last video, we found the eigenvectors for the matrix A = 3 over 2, 5 over 2, 3; minus 1 over 2, minus 3 over 2, minus 3; 1, 1, 2 to be:
-
for lambda = 1, x, minus 5 x, minus 4 x,
-
for lambda = 2, x, minus x, 0,
-
for lambda = minus 1, x, minus x, x
For the matrix 2, 1; 1, 1 we found the eigenvalue 3 plus or minus root 5, all over 2 had eigenvectors x, (minus 1 plus or minus root 5), all times x over 2. All of these have the free parameter x.
This is a general fact:
A times k v equals k A v, which equals k lambda v, which equals lambda times k v.
So for example, the vectors x, minus x, x are all just rescalings of 1, minus 1, 1. Indeed, people often say things like "the eigenvector is 1, minus 1, 1", when they mean "the eigenvectors are all the rescalings of 1, minus 1, 1". If you write this kind of thing in your answers, that's fine.
Suppose we have the matrix I = 1, 0; 0, 1. The characteristic polynomial is det of I minus lambda I equals det of 1 minus lambda, 0,; 0, 1 minus lambda, which equals (1 minus lambda) all squared, so lambda = 1 is the only eigenvalue. Any vector v satisfies I v = v, so any vector x, y is a 1-eigenvector. This has two free parameters, so it is an eigenplane, not just an eigenline: there is a whole plane of eigenvectors for the same eigenvalue.
The set of eigenvectors with eigenvalue lambda form a (complex) subspace of C^n (i.e. closed under complex rescalings and under addition).
Let V_lambda be the set of lambda-eigenvectors of A. If v is in V_lambda then k v is in V_lambda (as we saw above). If v_1, v_2 are both in V_lambda then A times v_1 + v_2 = A v_1 + A v_2 = lambda v_1 + lambda v_2, which equals lambda times (v_1 + v_2), so v_1 + v_2 is also a lambda-eigenvector.
We call this subspace the lambda-eigenspace. In all the examples we saw earlier (except I), the eigenspaces were 1-dimensional eigenlines (one free variable). So a matrix gives you a collection of preferred directions or subspaces (its eigenspaces), which tell you something about the matrix (e.g. if it's a rotation matrix, its axis will be one of these subspaces).
For the example 2, 1; 1, 1 we found the eigenvalues (3 plus or minus root 5), all over 2 and eigenvectors x, ((minus 1 plus or minus root 5), all times x over 2). We now draw these two eigenlines (in red).
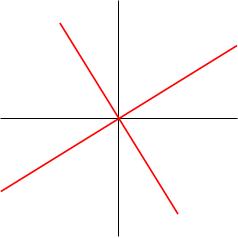
Note that these eigenlines look orthogonal; indeed, you can check that they are! You do this by taking the dot product of the eigenvectors (it's zero). This is true more generally for symmetric matrices (i.e. matrices A such that A = A transpose).