40. Images

Definition:

0.00 The image of a linear map $f\colon\mathbf{R}^{n}\to\mathbf{R}^{m}$ is the set of vectors $b\in\mathbf{R}^{m}$ such that $b=f(v)$ for some $v\in\mathbf{R}^{n}$ . It is written as $\mathrm{im}$ .

0.59 If you think of applying a map as "following light rays" (like in some earlier examples), you can think of the image as the shadow your map casts.

If the map $f$ is the vertical projection $f\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}x\\ y\\ 0\end{pmatrix}$ then the image of $f$ is the $x y$ -plane. That is $\mathrm{im}(f)=\left\{\begin{pmatrix}x\\ y\\ 0\end{pmatrix}\ :\ x,y\in\mathbf{R}\right\}.$

2.42 Consider the 3-by-2 matrix $A=\begin{pmatrix}1&1\\ 2&0\\ 0&1\end{pmatrix}$ . The image of the corresponding linear map is the set of all vectors of the form $A\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}x+y\\ 2x\\ y\end{pmatrix}.$ We studied this example earlier and even drew a picture of its image: it is the grey plane in the figure below. (There's a slight "videographic typo" (i.e. "mistake") in the video, see if you can spot it).

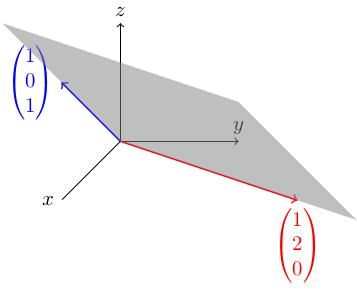
The plane of vectors of the form (x+y,2x,y) in 3D

Remarks

4.50 $0\in\mathrm{im}(f)$ because $0=f(0)$ .
If $f$ is invertible then $\mathrm{im}(f)=\mathbf{R}^{m}$ . This is because if $b\in\mathbf{R}^{m}$ then $b=f(f^{-1}(b))$ , so $b\in\mathrm{im}(f)$ .

Image is a subspace

Lemma:

6.08 The image of $f$ is a subspace.

If $b_{1},b_{2}\in\mathrm{im}(f)$ then so is $b_{1}+b_{2}$ . To see this, observe that if $b_{1},b_{2}\in\mathrm{im}(f)$ then $b_{1}=f(v_{1})$ and $b_{2}=f(v_{2})$ for some $v_{1},v_{2}\in\mathbf{R}^{n}$ . This means that $b_{1}+b_{2}=f(v_{1})+f(v_{2})=f(v_{1}+v_{2})$ (since $f$ is linear), so $b_{1}+b_{2}\in\mathrm{im}(f)$ .

7.14 Similarly, $\lambda b_{1}=\lambda f(v_{1})=f(\lambda v_{1})$ (since $f$ is linear), so $\lambda b_{1}\in\mathrm{im}(f)$ .

Relation with simultaneous equations

Lemma:

7.57 $Av=b$ has a solution if and only if $b\in\mathrm{im}(f)$ where $f(v)=Av$ .

This is a tautology from the definition of image! $Av=b$ has a solution if and only if there is a $v$ such that $f(v)=Av=b$ .

9.14 So putting this together with the last lecture, we see that $Av=b$ has a solution if and only if $b\in\mathrm{im}(f)$ and, if it has a solution, then the space of solutions is a translate of $\ker(f)$ .

Rank

Definition:

9.42 The rank of a linear map/matrix is the dimension of its image.

Theorem:

10.22 (Rank-nullity theorem) If $A$ is an $m$ -by- $n$ matrix (or $f\colon\mathbf{R}^{n}\to\mathbf{R}^{m}$ is a linear map) then $\mathrm{rank}(A)+\mathrm{nullity}(A)=n.$ Here $n$ is the number of columns or $A$ (or the dimension of the target of $f$ ).

11.29 The 3-by-3 matrix $A=\begin{pmatrix}0&0&0\\ 0&0&0\\ 0&0&0\end{pmatrix}$ sends everything to zero, so its image is a single point, which has dimension zero, so $\mathrm{rank}(A)=0$ . The kernel is the set of things which map to zero, and since everything maps to zero the kernel is $\mathbf{R}^{3}$ . Therefore the nullity (dimension of the kernel) is three. Note that $0+3=3$ and $n=3$ ( $A$ is a 3-by-3 matrix) so the rank-nullity theorem holds.

12.34 The 3-by-3 matrix $B=\begin{pmatrix}1&0&0\\ 0&0&0\\ 0&0&0\end{pmatrix}$ sends $\begin{pmatrix}x\\ y\\ z\end{pmatrix}$ to $\begin{pmatrix}x\\ 0\\ 0\end{pmatrix}$ , so its image is the $x$ -axis. Therefore the rank (dimension of the image) is 1. The nullity is the number of free variables ( $B$ is in reduced echelon form already) which is 2 (there is one leading entry). Again, $1+2=3$ , which is good. We can see that as the rank increases, the nullity goes down (as required by the rank-nullity theorem).

13.27 The matrix $C=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&0\end{pmatrix}$ is the vertical projection to the $x y$ -plane, so its rank is 2 (image is the $x y$ -plane). Its nullity is 1 (one free variable). Again, $2+1=3$ .

13.58 The 3-by-3 identity matrix $I=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}$ has rank 3 (for any $v$ we have $v=Iv$ so every vector is in the image) and the nullity is 0 (only the origin maps to the origin). Again, $3+0=3$ .

14.43 The rank-nullity theorem is basically saying that the map $f$ is taking $\mathbf{R}^{n}$ , crushing down some of the dimensions (those in the kernel), and mapping the rest faithfully onto the image (so the $n$ dimensions of $\mathbf{R}^{n}$ either contribute to the kernel or to the image).

Proof of rank-nullity theorem

15.17 The nullity of $A$ is the number of free variables of $A$ when you put it into reduced echelon form. If we can show that the rank is the number of dependent variables then we're done: there are $n$ variables which are either free (contributing to kernel) or dependent (contributing to rank). Recall that the dependent variables correspond to the columns with leading entries in reduced echelon form.

17.15 So we need to show that the rank is the number of leading entries of $A$ in reduced echelon form.

First step: we prove that the rank doesn't change when we do a row operation. Suppose we start with a matrix $A$ , do a row operation to get a matrix $A^{\prime}$ . We know there is an elementary matrix $E$ such that $A^{\prime}=EA$ . This tells us immediately that $\mathrm{im}(A)$ and $\mathrm{im}(A^{\prime})$ have the same dimension: $b\mapsto Eb$ gives us an "isomorphism" (invertible linear map) from the image of $A$ to the image of $A^{\prime}$ .

19.08 As the rank doesn't change under row operations, we may assume without loss of generality that $A$ is in reduced echelon form.

19.36 Second step: if $A$ is in reduced echelon form then it has $k$ nonzero rows (for some $k$ ) followed by $m-k$ zero rows. Now:

The number $k$ is the number of leading entries (because each nonzero row has a leading entry and each zero row doesn't).
Recall that $Av=b$ has a solution if and only if $b_{k+1}=b_{k+2}=\cdots=b_{m}=0$ : these are the necessary and sufficient conditions for solving the simultaneous equations. If $A$ has a zero row then $b$ has to have a zero in that row, and if all these higher $b$ s are zero then the other rows of $A$ just give us equations which determine the dependent variables.

21.07 Since the image of $A$ is the set of $b$ for which $Av=b$ has a solution, this means that $\mathrm{im}(A)$ is the set of $b$ for which $b_{k+1}=\cdots=b_{m}=0$ , i.e. those $b$ of the form $\begin{pmatrix}b_{1}\\ \vdots\\ b_{k}\\ 0\\ \vdots\\ 0\end{pmatrix}$ . This is a $k$ -dimensional space, so we see that the rank equals $k$ , the number of leading entries.

This completes the proof of the rank-nullity theorem.