39. Kernels

Definition of the kernel

0.00 Recall the following definitions:

Definition:

$f$ is a linear map if

$f(v+w)=f(v)+f(w)$ for all $v, w$
$f(\lambda v)=\lambda f(v)$ for all $v$ and all $\lambda\in\mathbf{R}$ .

Definition:

$V$ is a linear subspace if

$v,w\in V$ implies $v+w\in V$
$v\in V$ implies $\lambda v\in V$ for all $\lambda\in\mathbf{R}$ .

0.50 These two definitions are very similar. We will exploit this in the next two videos: given a linear map $f\colon\mathbf{R}^{n}\to\mathbf{R}^{m}$ , we will associate to it two subspaces $\ker(f)\subset\mathbf{R}^{n}$ (the kernel of $f$ ) and $\mathrm{im}(f)$ (the image of $f$ ).

Definition:

1.50 The kernel of $f$ is the set of $v\in\mathbf{R}^{n}$ such that $f(v)=0$ . (If $m=n$ then this is just the 0-eigenspace of $f$ ).

Example:

2.28 Let $f\colon\mathbf{R}^{3}\to\mathbf{R}^{3}$ be the map $f(v)=Av$ for $A=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&0\end{pmatrix}$ . Note that $f\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}x\\ y\\ 0\end{pmatrix}$ . This is the vertical projection to the $x y$ -plane.

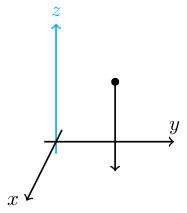
3.45 The kernel of $f$ is the $z$ -axis (blue in the figure; these are the points which project vertically down to the origin). That is $\mathrm{ker}(f)=\left\{\begin{pmatrix}0\\ 0\\ z\end{pmatrix}\ :\ z\in\mathbf{R}\right\}$ .

Example:

4.30 Recall the example $A=\begin{pmatrix}1&0&-1\\ 0&1&-1\end{pmatrix}$ (going from $\mathbf{R}^{3}$ to $\mathbf{R}^{2}$ ) from Video 3. This projects vectors into the plane; if we think of $\mathbf{R}^{2}$ as the $x y$ -plane then we can visualise this map as the projection of vectors in the $\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}$ -direction until they live in the $x y$ -plane.

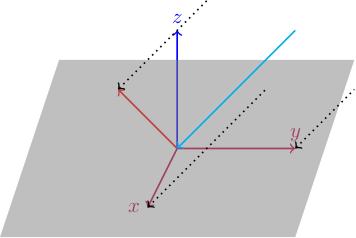
6.00 We described this as projecting light rays in the $\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}$ direction. In this case, the kernel of $A$ is precisely the light ray which hits the origin, which is the line $\left\{\begin{pmatrix}x\\ x\\ x\end{pmatrix}\ :\ x\in\mathbf{R}\right\}$ (light blue in the picture).

Kernel is a subspace

Lemma:

7.23 The kernel is a subspace.

Given $v,w\in\ker(f)$ , we need to show that $v+w\in\ker(f)$ . Since $v,w\in\ker(f)$ , we know that $f(v)=f(w)=0$ . Therefore $f(v+w)=f(v)+f(w)$ (since $f$ is linear) $=0+0=0$ , so $v+w\in\ker(f)$ . Similarly, $f(\lambda v)=\lambda f(v)=\lambda 0=0$ .

Remarks

9.17 $0\in\ker(f)$ for any linear map $f$ because $f(0)=0$ .
If $f$ is invertible then $\ker(f)=\{0\}$ : if $v\in\ker(f)$ then $v=f^{-1}(0)=0$ .
10.17 The "kernel" in a nut is the little bit in the middle that's left when you strip away the husk. If $f(v)=Av$ then we can think of $\ker(f)$ as the space of solutions to the simultaneous equations $Av=0$ , which is the intersection of the hyperplanes
$A_{11}v_{1}+\cdots+A_{1n}v_{n}=0,\cdots,A_{m1}v_{1}+\cdots+A_{mn}v_{n}=0.$ In other words, it's the little bit left over when you've intersected all these hyperplanes.

Simultaneous equations revisited

Lemma:

12.29 Consider the simultaneous equations $Av=b$ ( $A$ is an $m$ -by- $n$ matrix and $b\in\mathbf{R}^{m}$ ). Let $f(v)=Av$ . The space of solutions to $Av=b$ , if nonempty, is an affine translate of $\ker(f)$ .

Example:

14.08 If $A=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&0\end{pmatrix}$ (so $f$ is vertical projection to the $x y$ -plane) then $Av=b$ has a solution only if $b$ is in the $x y$ -plane, and in that case it has a whole vertical line of solutions sitting above $b$ .

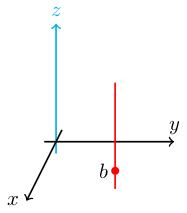
This vertical line of solutions is parallel to the kernel of $f$ (the $z$ -axis), i.e. it is a translate of the kernel.

16.05 We saw this lemma earlier in a different guise in Video 19. Namely, we saw that if $v_{0}$ is a solution to $Av=b$ then the set of all solutions is the affine subspace $v_{0}+U$ where $U$ is the space of solutions to $Av=0$ . In other words, $U=\ker(f)$ .

17.37 In particular, we see that if $Av=b$ has a solution then it has a $k$ -dimensional space of solutions, where $k$ is the dimension of $\ker(f)$ .

18.54 Remember that the space of solutions has dimension equal to the number of free variables when we put $A$ into reduced echelon form. For example, $A=\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&0\end{pmatrix}$ is in reduced echelon form with two leading entries and one free variable, which is why we get 1-dimensional solution spaces.

Definition:

19.55 The nullity of $A$ (or of $f$ ) is the dimension of $\ker(f)$ (i.e. the number of free variables of $A$ when put into reduced echelon form).

Our goal for the next video is to prove the rank-nullity theorem which gives us a nice formula relating the nullity to another important number called the rank.