Determinants and volumes, revisited

Determinants and volumes, revisited

0.00 In an earlier video, we claimed that the determinant of a matrix $M$ is equal to the volume of the parallelopiped which is the image of the unit cube under the linear transformation associated with $M$ . We saw a proof of this for 2-by-2 matrices, but it wasn't clear how to generalise this to higher dimensions. In this video we will see another proof in 2-dimensions, one whose generalisation to higher dimensions is hopefully clearer.

0.50 The unit cube has vertices at $(0,0)$ , $(1,0)$ , $(0,1)$ and $(1,1)$ . If we apply the 2-by-2 matrix then the vertices become $(0,0)$ , $(a,c)$ , $(b,d)$ and $(a+b,c+d)$ .

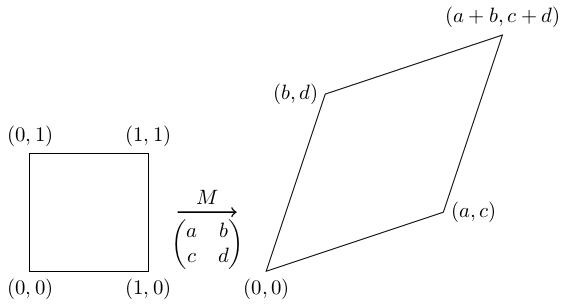
We will calculate the volume (area) of this parallelogram by rearrangement: cutting it into pieces and rearranging them using translations. The fact that the volume doesn't change when we do this is known as Cavalieri's principle.

02.18 We will cut the parallelogram into layers parallel to the edge connecting the origin to $(a,c)$ . Then we will slide these layers in the $(-a,-c)$ direction (i.e. along themselves) until they line up along the $y$ -axis.

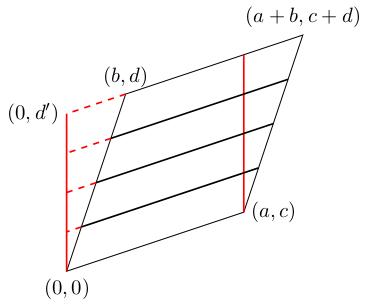
3.00 The result of this is a new parallelogram such that two of its edges are vertical and the other two are still parallel to $(a,c)$ . Indeed, two vertices are still at the origin and at $(a,c)$ , but the vertex at $(b,d)$ has now moved a certain amount (let's say $-m$ ) parallel to the $(a,c)$ -direction, so that it is now at $(b-ma,d-mc)$ . What is $m$ ? It's whatever it needs to be to make the first coordinate of this point equal to zero, so that it sits on the $y$ -axis. In other words, this corner is at $(0,d^{\prime })$ where $d^{\prime }=d-mc$ .

4.30 In terms of the matrix $M$ , we have subtracted off $m$ times the first column from the second column to "clear" the top entry of the second column (make it equal to zero): $$C_2\mapsto C_2-m{C}_1.$$

4.55 We do one more rearrangement (in higher dimensions we'd need to do more). Namely, we split the parallelogram into vertical slices and translate them vertically down until they line up along the $x$ -axis. The result is a rectangle base $a$ and height $d^{\prime }$ .

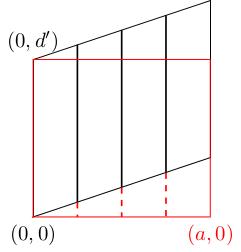
5.40 In terms of $M$ , we have already done a column operation to get and we now subtract off some multiple of column 2 from column 1 to get a diagonal matrix . The volume (area) of the parallelogram we started with is the same as the area of this rectangle (because rearrangements don't change volumes) and this equals $a{d}^{\prime }$ , the determinant of this diagonal matrix. But this is equal to the determinant of $M$ because, just like row operations, column operations don't change the determinant.