The Lie algebra of a matrix group

Our goal

We have introduced the exponential map exp from little g l n R to big G L n R This map has some nice properties:

Our goal is to construct a replacement little g for little g l n R when we replace big G L n R by a suitable group big G. We also want an exponential map exp from little g to big G which satisfies the properties above, and to make sense of the BCH formula, we need little g to have a bracket operation.

Example:

Let G equals U(1) equals the set of complex numbers z with length 1 be the set of unit complex numbers. This is a group: if you multiply two elements of U(1) together you get another unit complex number. Geometrically, it's a circle in the complex plane.

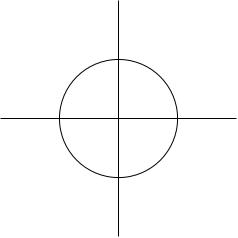
The unit circle in C

Any z in U(1) can be written as z equals e to the i theta for some \theta. The map i\theta\mapsto e^{i\theta} is going to be our exponential map in this example and it goes from the imaginary numbers i R to U(1). The commutator bracket on i R vanishes: i theta 1 bracket i theta 2 equals minus theta 1 theta 2 plus theta 2 theta 1 equals zero, and the Baker-Campbell-Hausdorff formula reduces to the usual law of logarithms e to the i theta 1 times e to the i theta 2 equals e to the i (theta 1 plus theta 2).

If we translate the line of imaginary numbers so that it passes through the identity element 1 in U(1) then we get a tangent line to the circle U(1). This will be true in general: little g will be (parallel to) the tangent space to G at the identity.

The tangent line to U(1) is parallel to the imaginary axis

The Lie algebra of a matrix Lie group

Here is the theorem we're aiming for; we'll prove it in a later video and I'll spend the rest of this video discussing the new words in the statement of the theorem.

Theorem:

Let G be a topologically closed subgroup of big G L n R. Define little g to be the set of matrices X in little g l n R such that exp (t X) is in G for all t in R. (In particular, exp(X) is in G for all X in little g.) Then:

  1. little g is a vector space; this may seem odd because little g consists of matrices, not vectors, but remember that abstractly a vector space is just something whose elements you can add and rescale (which you can do with matrices). In particular, little g l n R is a vector space, and little g will be a subspace.

  2. The commutator bracket restricts to give an operation on little g, i.e. if X and Y are in little g then X bracket Y is in little g.

  3. little g is parallel to the tangent space of G at the identity matrix.

  4. exp from little g to big G is locally invertible, i.e. there are neighbourhoods U of 0 in little g and V of the identity in big G and an inverse log from V to U for \exp.

little g is called the Lie algebra of G, and it's usually a much simpler object than G.

Some remarks

Remark:

Topologically closed subgroups of big G L n R are instances of a more general mathematical entity called a Lie group. This basically means that they are groups which admit local coordinate systems for which the group multiplication map and the map g goes to g^{-1} are differentiable maps. There are examples of Lie groups which don't arise as topologically closed subgroups of big G L n R, but most of the interesting ones do arise this way, so we won't lose out on much by restricting attention to topologically closed groups of matrices. This narrowed focus will make our lives much easier in many ways. You can learn about smooth manifolds and Lie groups in your in-depth project if you want.

Definition:

A subgroup G inside big G L n R is topologically closed if for any sequence g 1, g 2, dot dot dot is a sequence of elements of G such that g k converges in big G L n R then the limit lim as k goes to infinity of g k lies in G.

Example:

The group big G L n Q is a subgroup of big G L n R but it is not topologically closed: the sequence of rational matrices 3, 0, 0, 1; 3.1, 0, 0, 1; 3.14, 0, 0, 1; etc converges to pi, 0, 0, 1, which is not in G L n Q.

Why do I want to throw examples like this away? In this example, little g would be 0, but any neighbourhood of the identity in G L n Q contains infinitely many matrices, so it's not possible for the exponential map to be locally invertible in the sense of the theorem.

If you want to work with groups like G L n Q then you should use the theory of algebraic groups instead.

Remark:

If G inside G L n R is a subgroup then its topological closure G bar is a topologically closed subgroup. The topological closure is obtained by adding in all the limit points of sequences in G; this is obviously topologically closed, and I'm claiming that it's still a subgroup (this will be an exercise).

Definition (Matrix groups):

In what follows, we will use the word matrix group or matrix Lie group to mean a topologically closed subgroup of G L n R.

We will only focus on matrix groups, and this will allow us to move quickly on to the representation theory of groups we care about rather than faffing around introducing manifolds.