Linearity of homomorphisms in exponential charts

1.20 Our first observation is that, for all $X\in 𝔤$ , $\exp (tX)$ is a 1-parameter subgroup. Since $F$ is a smooth homomorphism, and since a 1-parameter subgroup is just a smooth homomorphism from $𝐑$ , we deduce that $F(\exp (tX))$ is a 1-parameter subgroup in $H$ . By what we proved about 1-parameter subgroups, $F(\exp (tX))=\exp (tY)$ for some $Y\in 𝔥$ .

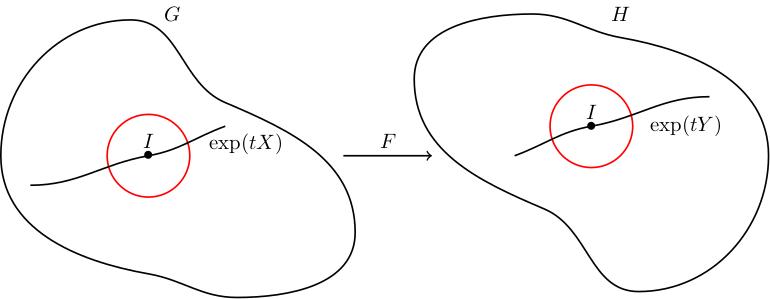
2.40 The figure above shows the groups $G$ and $H$ , the paths $\exp (tX)$ and $\exp (tY)$ , and (red) neighbourhoods of the identity in each on which the logarithm is well-defined. For small $t$ , $\exp (tX)$ and $\exp (tY)$ are both close to the identity, so live in the domain of the local logarithm.

4.20 We have $F(\exp (tX))=\exp (f(tX))$ for small $t$ and $F(\exp (tX))=\exp (tY)$ for all $t$ . Therefore, for small $t$ we can take logarithms and deduce that $f(tX)=tY$ .

5.30 Since $f$ is a smooth map, we can take the Taylor series $f(tX)=t{d}_{0}f(X)+\text{higher order in }t$ , where $d_{0}f$ is the derivative of $f$ at $0$ . Because $f(tX)=tY$ , we see that $d_{0}f(X)=Y$ and all higher order terms vanish.

7.00 This means that $f(tX)=tY=t{d}_{0}f(X)=d_{0}f(tX)$ for all $X$ and all sufficiently small $t$ . Therefore $f=d_{0}f$ on the domain of the exponential chart. We take $F_{*}=d_{0}f$ . This proves the first part of the theorem. Recall that the matrix for the linear map $d_{0}f$ is the matrix of partial derivatives of components of $f$ , $$d_{0}f=\left(\frac{\partial f_i}{\partial x_j}\right).$$

8.35 The second part follows from what we have already said: we showed that $F(\exp tX)=\exp (tY)$ (for all $t$ ), and $Y=d_{0}f(X)=F_{*}(X)$ . Setting $t=1$ we get $F(\exp X)=\exp (F_{*}(X))$ .

9.55 To prove the final part of the theorem, consider the expression $$\exp (tX)\exp (tY)\exp (-tX)\exp (-tY)$$ Use the Baker-Campbell-Hausdorff formula to multiply the first two and last two terms together and we get $$\exp \left(t(X+Y)+\frac{1}{2}{t}^2[X,Y]+\mathrm{\cdots }\right)\exp \left(-t(X+Y)+\frac{1}{2}{t}^2[X,Y]+\mathrm{\cdots }\right)$$ 11.15 Using the Baker-Campbell-Hausdorff formula to multiply these two together, after a little manipulation, we get $$\exp (t^2[X,Y]+𝒪(t^3)).$$

12.00 If I apply $F$ to this whole expression, we get: $$F(\exp (t^2[X,Y]+𝒪(t^3)))=\exp (t^2{F}_{*}[X,Y]+𝒪(t^3))$$ by definition of $F_{*}$ .

12.35 Because $F$ is a homomorphism, $$F(\exp (tX)\exp (tY)\exp (-tX)\exp (-tY))=F(\exp (tX))F(\exp (tY))F(\exp (-tX))F(\exp (-tY)).$$ By definition of $F_{*}$ , this equals $\exp (t{F}_{*}X)\exp (t{F}_{*}Y)\exp (-t{F}_{*}X)\exp (-t{F}_{*}Y)$ and using the Baker-Campbell-Hausdorff formula in the same way we get $$\exp (t^2[F_{*}X,F_{*}Y]+𝒪({𝓉}^{\mathcal{3}}))$$

13.45 If we take $t$ small then we can take logarithms and we get $$t^2[F_{*}X,F_{*}Y]=t^2{F}_{*}[X,Y]+𝒪(t^3).$$ Differentiating twice and setting $t=0$ we get $F_{*}[X,Y]=[F_{*}X,F_{*}Y]$ as required.