Lie's theorem on homomorphisms

Exponentiating homomorphisms

0.00 Last time we proved the following theorem.

Theorem:

If $F\colon G\to H$ is a homomorphism of Lie groups then there exists a linear map $F_{*}\colon\mathfrak{g}\to\mathfrak{h}$ which is a Lie algebra homomorphism (i.e. $F_{*}[X,Y]=[F_{*}X,F_{*}Y]$ ) such that $F(\exp X)=\exp(F_{*}X)$ for all $X\in\mathfrak{g}$ .

0.45 What about the other direction? If we're given a Lie algebra homomorphism $f\colon\mathfrak{g}\to\mathfrak{h}$ , can we find a Lie group homomorphism $F\colon G\to H$ such that $F_{*}=f$ ?

Example:

1.00 Take $G=H=U(1)$ . Then $\mathfrak{g}=\mathfrak{h}=i\mathbf{R}$ so, for any smooth homomorphism $F\colon U(1)\to U(1)$ we get $F_{*}\colon i\mathbf{R}\to i\mathbf{R}$ . Since $F_{*}$ is linear and $i\mathbf{R}$ is 1-dimensional, $F_{*}(i\theta)=i\lambda\theta$ for some $\lambda\in\mathbf{R}$ .

2.15 The Lie bracket on $i\mathbf{R}$ is trivial: $[i\theta_{1},i\theta_{2}]=i^{2}\theta_{1}\theta_{2}-i^{2}\theta_{2}\theta_{1}=0$ , so $F_{*}$ automatically preserves the bracket. Therefore any $\lambda$ defines for us a Lie algebra homomorphism $i\mathbf{R}\to i\mathbf{R}$ , $i\theta\mapsto i\lambda\theta$ .

2.55 So any homomorphism $F\colon U(1)\to U(1)$ has the form $F(e^{i\theta})=e^{i\lambda\theta}$ for some $\lambda$ . Which $\lambda$ can occur? Not all of them. For $F$ to be well-defined, we need $F(e^{i2\pi})=F(1)$ (because $e^{i2\pi}=1$ ) so we need $e^{i2\pi\lambda}=1$ and hence we need $\lambda\in\mathbf{Z}$ . Conversely, if $\lambda\in\mathbf{Z}$ then $F(e^{i\theta})=e^{i\lambda\theta}$ is well-defined: it's just raising $e^{i\theta}$ to the (integer) power $\lambda$ .

3.55 So not every Lie algebra homomorphism can be exponentiated to get a Lie group homomorphism: $i\theta\mapsto i\lambda\theta$ can be exponentiated if and only if $\lambda\in\mathbf{Z}$ .

This example is sufficiently important to summarise as a lemma:

Lemma:

4.20 The maps $F_{n}(e^{i\theta})=e^{in\theta}$ , $n\in\mathbf{Z}$ , are homomorphisms $U(1)\to U(1)$ and every smooth homomorphism $U(1)\to U(1)$ is one of these.

5.00 The integers come into this example because the group $U(1)$ has some interesting topology. $U(1)$ is a circle, so loops in $U(1)$ have a winding number that counts how many times they go around the circle. The $\mathbf{Z}$ in the lemma is related to this integer winding number.

Simply-connectedness

5.55 There is a topological condition you can put on $G$ to ensure that any Lie algebra homomorphism exponentiates.

Theorem (Lie):

Let $G$ be a simply-connected matrix group and $H$ any matrix group. Then for every Lie algebra homomorphism $f\colon\mathfrak{g}\to\mathfrak{h}$ there exists a smooth group homomorphism $F\colon G\to H$ such that $F_{*}=f$ .

We will not prove this theorem: it's a gorgeous proof and would make an excellent project!

Definition:

8.00 A space $X$ is called simply-connected if, for every loop $\gamma$ in $X$ there is a nullhomotopy of $\gamma$ .

Definition:

8.45 A loop in $X$ is a continuous map $\gamma\colon[0,1]\to X$ such that $\gamma(0)=\gamma(1)$ . You should think of $\gamma(t)$ as a parametrised path with parameter $t\in[0,1]$ , which starts and ends at the same point. If $X$ is a matrix group then continuity here means that the matrix entries of $\gamma(t)$ depend continuously on $t$ .

Definition:

9.30 A nullhomotopy of a loop $\gamma$ is a continuous map $H\colon[0,1]\times[0,1]\to X$ (which we can think of as a family of loops $\gamma_{s}(t)=H(s,t)$ ) such that:

these loops all start and end at the same point $x$ (so $H(s,0)=H(s,1)=x$ for all $s\in[0,1]$ .
$\gamma_{0}(t)=H(0,t)$ is our loop $\gamma(t)$
$\gamma_{1}(t)=H(1,t)$ is the constant loop $H(1,t)=x$ .

In other words, $\gamma_{s}(t)$ starts being $\gamma$ and gradually shrinks down to a constant loop.

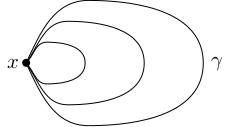
A nullhomotopy is a sequence of loops shrinking to a point

11.40 The circle is certainly not simply-connected, but there are plenty of groups which are simply-connected. There is an optional video which talks more about the topology of the groups we've been meeting which will give a vague explanation for why the groups $SU(n)$ are simply-connected. I also have some videos about topology, simply-connectedness and the fundamental group if you want to learn more about this (you could do a project about the topology of Lie groups).