We now turn to the representation theory of the group SU(2), which is the simplest nonabelian Lie group. Recall that SU(2) is the group of special unitary 2-by-2 matrices, that is: SU(2) = the set of M such that M dagger M equals the identity and det M equals 1 where M dagger denotes the conjugate-transpose of M. There's a nice way of writing down all the matrices in SU(2), namely: SU(2) equals the set of matrices a, b, minus b bar, a bar where absolute value of a squared plus absolute value of b squared equals 1 This is a 3-dimensional group because there are four variables (real and imaginary parts of a and b) and one real condition absolute value of a squared plus absolute value of b squared equals 1, so overall there are three degrees of freedom. You can also see this from the Lie algebra: little s u 2 equals the set of matrices X such that X dagger equals minus X and trace of X equals zero You can write the matrices from little s u 2 in the following form: little s u 2 equals the set of matrices of the form i x, y plus i z, minus y plus i z, minus i x, where x,y,z are real The fact that the diagonal entries are imaginary and that the off-diagonal entries are related by a sign-change in the real part are coming from X dagger equals minus X; the fact that the diagonal entries sum to zero is trace of X equals zero.
Note that x, y and z are real so there are 3 real coordinates and it's a 3-dimensional Lie algebra. If v equals the vector x, y, z, we will write M_v equals the matrix ix, y plus i z, minus y plus i z, minus i x.
What representations of SU(2) do we already know? A representation is a way of representing group elements as matrices, and our group elements are already matrices, so there is the "standard representation" SU(2) to G L 2 C, sending a, b, minus b bar, a bar to itself This is a 2-dimensional complex representation.
We also encountered the following representation SU(2) to GL of little s u 2, representing g by the map sending M_v to g M_v g inverse In other words, each element g in SU(2) is represented by the linear map from little s u 2 to little s u 2 which sends M_v to g M_v g inverse.
If V is a vector space, then GL(V) will denote the set of invertible linear maps V to V. This is a handy piece of notation as it allows us to keep track of precisely which vector space we're acting on. For example, GL(C 3) equals G L 3 C, but the notation G L 3 C only remembers the dimension of the vector space and the field we're working over, not the name of the vector space we're using.
This representation SU(2) to GL of little s u 2 is 3-dimensional because the vector space little s u 2 is 3-dimensional. It is, however, a real representation, and we're really interested in complex representations, so I'll modify it slightly. We will complexify little s u 2 and replace it by little s u 2 tensor C, in other words the set of matrices i x, y plus i z, minus y plus i z, minus i x where x, y and z are complex numbers. This gives us a complex 3-dimensional representation.
Are there any more representations?
There is the trivial 1-dimensional representation S U 2 to G L 1 C, which sends every element to the 1-by-1 identity matrix. This is irreducible (it has no proper subspaces, let alone proper subrepresentations).
There is also the zero representation on the 0-dimensional vector space 0, which sends every matrix to the identity (a 0-dimensional vector space is just the origin with no axes, so the identity is just the map which sends the origin to the origin: there's no sensible way of writing this as a matrix).
We now have complex representations of dimension 0, 1, 2 and 3. It turns out that there is a unique irreducible representation in each dimension.
For any nonnegative integer n there is an n-dimensional irreducible representation ("irrep") R subscript n from SU(2) to G L n C. Moreover, any irrep R from S U 2 to G L V is isomorphic to one of these.
The proof of the theorem will take several videos. In what remains of this video, we will define the word "isomorphic". In the next video, I'll construct the irreps R subscript n. It will then take us four videos to analyse the representations enough to prove the theorem.
Given two representations R from G to G L V and S from G to G L W of the same group G on vector spaces V and W, a
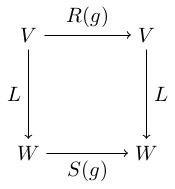
It's called an
If V equals W equals C n and L is an isomorphism then we can think of L as a change-of-basis matrix. The fact that S of g equals L compose R of g compose L inverse is saying that, with respect to the new basis, the matrices R of g become the matrices S of g. So two representations are isomorphic if they are given by the same matrices with respect to some choice of basis.
Consider the representations:
R from U(1) to G L 2 C, R of e to the i theta equals cos theta, minus sine theta, sine theta, cos theta
S from U(1) to G L 2 C, S of e to the i theta equals the diagonal matrix with diagonal entries e to the i theta, e to the minus i theta.
We saw in an earlier video that S is obtained from R by changing to a basis of simultaneous eigenvectors i, 1 and minus i, i. The change of basis matrix is L equals the matrix i, minus i, 1, 1. We will check that R of g equals L compose S of g compose L inverse, so L defines an isomorphism S to R.
We have: L inverse equals the inverse of i, -i, 1, 1, equals one over 2 i times the matrix 1, i, minus 1, i and the matrix product L compose S of g compose L inverse reduces to R of g because cos theta equals (e to the i theta plus e to the minus i theta) all over 2, and sine theta equals (e to the i theta minus e to the minus i theta) all over 2 i.
Check that 1 over 2 i times the 2-by-2 matrix i, -i; 1, 1, times the 2-by-2 matrix e to the i theta, 0; 0, e to the minus i theta, times the 2-by-2 matrix 1, i; minus 1, i, equals cos theta, minus sine theta; sine theta, cos theta