Duals

Definition

Definition:

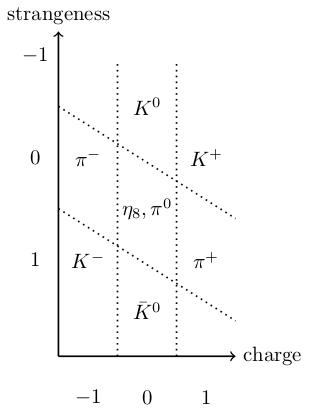
0.00 Given a representation $R\colon G\to GL(V)$ , the dual representation $R^{*}\colon G\to GL(V^{*})$ is defined as follows.

0.30 The dual vector space $V^{*}$ is the space $\mathrm{hom}(V,\mathbf{C})$ of linear maps from $V$ to $\mathbf{C}$ . Equivalently, if we think of $V$ as a space of column vectors by picking a basis of $V$ then we can think of $V^{*}$ as the space of row vectors: given an element $\alpha\in\mathrm{hom}(V,\mathbf{C})$ , we get a row vector $\underline{\alpha}$ as follows. Pick a basis of $V$ so that elements can be written as column vectors $v=\begin{pmatrix}v_{1}\\ \vdots\\ v_{n}\end{pmatrix}$ . Then $\alpha(v)=\alpha_{1}v_{1}+\cdots+\alpha_{n}v_{n}$ for some coefficients $\alpha_{i}$ . Define $\underline{\alpha}=\begin{pmatrix}\alpha_{1}&\cdots&\alpha_{n}\end{pmatrix}$ (so $\alpha(v)=\underline{\alpha}\cdot v$ ).

1.45 Conversely, if you have a row vector $w=\begin{pmatrix}w_{1}&\cdots&w_{n}\end{pmatrix}$ then we get the linear map $\bar{w}\in\mathrm{hom}(V,\mathbf{C})$ , defined by $\bar{w}(v)=w_{1}v_{1}+\cdots+w_{n}v_{n}$ .
2.25 The dual representation is defined as follows. For each $g\in G$ , define $R^{*}(g)\colon V^{*}\to V^{*}$ to be the map which sends a row vector $\underline{\alpha}$ to $\underline{\alpha}R(g)^{-1}$ . In other words, $\underline{R^{*}(g)\alpha}=\underline{\alpha}R(g)^{-1}.$

3.20 The messing with underlines is just to distinguish between applying a linear map and multiplying a matrix, because we want to multiply on the right.

Lemma:

4.10 This defines a representation.

Proof:

We have $\underline{R^{*}(g_{1}g_{2})\alpha}=\underline{\alpha}R(g_{1}g_{2})^{-1}=% \underline{\alpha}R(g_{2})^{-1}R(g_{1})^{-1}$ . But $\underline{\alpha}R(g_{2})^{-1}=\underline{R^{*}(g_{2})\alpha},$ and so $\underline{\alpha}R(g_{2})^{-1}R(g_{1})^{-1}=\underline{R^{*}(g_{1})R^{*}(g_{2% })\alpha}.$ Therefore $R^{*}(g_{1}g_{2})=R^{*}(g_{1})R^{*}(g_{2})$ as required.

Examples

SU(2) representations

Lemma:

5.45 If $R\colon SU(2)\to GL(V)$ is a complex representation with a given weight diagram $D$ then $R^{*}$ has the weight diagram $D^{*}=D$ .

Remark:

6.35 We will prove that the weights of $D^{*}$ are given by minus the weights of $D$ . Since weight diagrams of $SU(2)$ representations are symmetric about the origin, this means $D=D^{*}$ . By our classification theorem for $SU(2)$ representations, we deduce that $R\cong R^{*}$ for any $SU(2)$ -representation.

Proof:

7.00 Let $W_{n}$ be the weight space with weight $n$ . Recall that $v\in W_{n}$ then $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}v=e^{in\theta}v$ . If we apply $\dagger$ (conjugate transpose) to both sides of the equation, we get: $v^{\dagger}R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}^{\dagger}=e^{-in\theta}v^{\dagger}.$

7.50 Now $v^{\dagger}$ is the row vector $\begin{pmatrix}\bar{v}_{1}&\cdots&\bar{v}_{k}\end{pmatrix}$ .

8.10 We have an invariant Hermitian inner product on our representation. If we pick a basis which is orthonormal with respect to that then the matrices $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ of our representation (with respect to this basis) will be unitary, that is $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}^{\dagger}=R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{i\theta}\end{pmatrix}^{-1}$ . In other words, this is the matrix which, when acting on the right on row vectors, defines $R^{*}\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ .

9.15 This tells us that $v^{\dagger}\in V^{*}$ is a weight vector of $R^{*}$ with weight $-n$ , so the weights of $R^{*}$ are minus the weights of $R$ . Since the weights of $R$ are symmetric around the origin, this implies $D=D^{*}$ and $R^{*}\cong R$ .

SU(3) representations

10.15 For $SU(3)$ , the same argument tells us that the weights of $R^{*}$ are minus the weights of $R$ .

Example:

If $V$ is the standard representation then its weight diagram is

Weight diagram of standard rep of SU(3): vertices at L_1, L_2, L_3

so its dual has the following weight diagram:

Weight diagram of the dual of the standard rep of SU(3): vertices at minus L_1, minus L_2, minus L_3

10.45 Since these diagrams are different, $V$ is not isomorphic to $V^{*}$ .

Mesons

11.05 The quark model we discussed earlier can be extended to allow both quarks and antiquarks: antiquarks live in the dual of the standard representation. A meson is then a particle obtained by combining one quark and one antiquark, so lives in $\mathbf{C}^{3}\otimes(\mathbf{C}^{3})^{*}$ . It's an exercise to see that this decomposes as $\Gamma_{1,1}\oplus\mathbf{C}$ . This corresponds to the classification of mesons:

There are 8 particles in an octet (shown) and one particle ( $\eta_{1}$ ) in a singlet (with both strangeness and charge zero).

Pre-class exercise

Exercise:

Find the weight diagram of $\mathbf{C}^{3}\otimes(\mathbf{C}^{3})^{*}$ and verify that it decomposes as $\Gamma_{1,1}\oplus\mathbf{C}$ as claimed.