Quarks

Baryons

0.00 We've just decomposed the tensor cube of the standard representation of $SU(3)$ into its irreducible summands: $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}\cong\Gamma_{3,0}% \oplus\Gamma_{1,1}\oplus\Gamma_{1,1}\oplus\mathbf{C}.$ The weight diagrams for the irreps $\Gamma_{3,0}$ and $\Gamma_{1,1}$ are:

0.35 Now for something completely different. Here are some tables of subatomic particles.

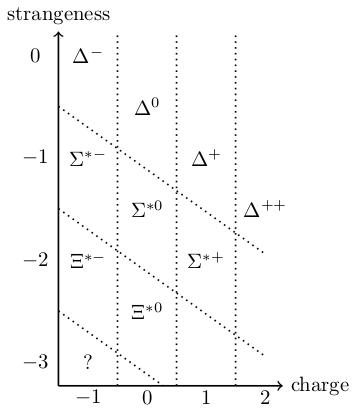
Baryons with spin 3/2, forming a triangle. In the first column with charge 1 we have three particles with strangeness going from 0 at the top to minus 2 at the bottom, and a hypothetical particle with strangeness minus 3 at the very bottom. In the second column with charge 0 we have three particles with strangeness going from 0 at the top to minus 2 at the bottom. In the third column with charge 1 we have two particles with strangeness 0 and minus 1. In the fourth an final column we have a particle with strangeness 0 and charge 2.

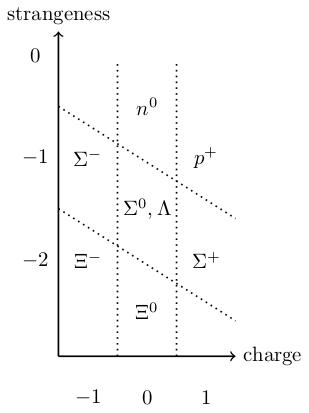
Baryons with spin a half, forming a hexagon. In the first column, with charge minus 1, we have two particles: one with strangeness minus 1 and one with strangeness minus 2. In the second column, with charge 0, we have one particle (the neutron) with strangeness 0, two with strangeness minus 1 and one with strangeness minus 2. In the third and final column, with charge 1, we have two particles, one (the proton) with strangeness 0 and one with strangeness minus 1.

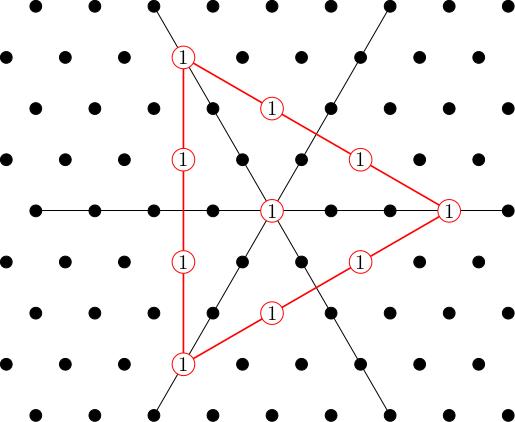
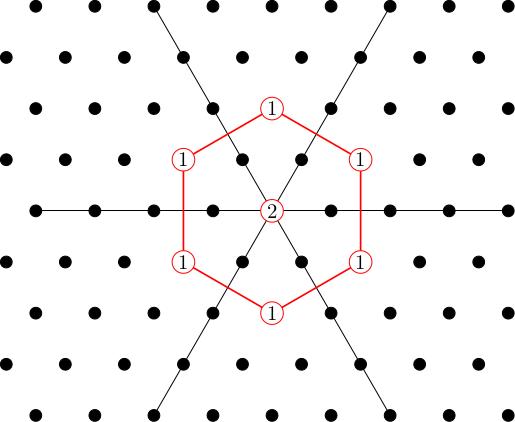
These are baryons (i.e. heavy particles) like protons ( $p$ in the table) and neutrons ( $n$ in the table). But there are also other weird particles with names like $\Delta^{-}$ or $\Xi^{*0}$ . They were discovered in particle accelerators in the 1950s and posed something of a mystery. People knew that protons and neutrons played an important role in nuclei of atoms, but what were all these other particles doing? Could they be classified?

1.25 In the diagrams above, we have grouped the particles into two sets according to their spin: those on the left have spin $3/2$ , those on the right have spin $1/2$ . Spin is a property of particles which you should think of as like an internal angular momentum for the particle: you could measure it by putting the particle into a magnetic field and observing its motion. Within each of these two sets, we have sorted them according to two more quantum numbers: the electric charge and the strangeness.

Remark:

2.25 What is strangeness? You could imagine a neutral particle decaying into two particles, one positively charged and one negatively charged. That would be OK because net charge would be preserved. However, there are some decays which obey charge conservation but which are nonetheless never observed. Physicists have postulated the existence of other conserved quantities which rule out these decay modes or interactions. Strangeness is one such quantity.

The quark model

3.30 There is a striking similarity between the weight diagrams occurring in the decomposition of $(\mathbf{C}^{3})^{\otimes 3}$ and the tables of baryons:

$\Gamma_{3,0}$ is a triangle (4 dots, 3 dots, 2 dots, 1 dot) with multiplicity 1 at each vertex; the spin $3/2$ baryons form the same triangle with 1 particle at each vertex. The only difference is the missing vertex at the bottom left (a missing particle with charge $-1$ and strangeness $-3$ ).
$\Gamma_{1,1}$ is a hexagon with multiplicity 1 at each vertex and multiplicity 2 at the origin; the spin $1/2$ baryons form a hexagon with one particle over every vertex and two over the origin.

4.10 In the early 1960s, Gell-Mann and Ne'eman independently arrived at the idea that this is not a coincidence. They predicted that the missing baryon should exist, and gave an explanation of where the classification scheme is coming from (EDIT: the description in terms of quarks actually came a couple of years after the link to $SU(3)$ representations had been observed). The missing baryon (the $\Omega^{-}$ baryon) was finally observed a couple of years later.

5.00 The proposal is that each of these particles should be made up of three smaller particles called quarks. Each quark corresponds to one of the three $\mathbf{C}^{3}$ factors in $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}$ . Each quark has three possible flavours: "up", "down" and "strange". This just refers to particular combinations of other properties like charge and strangeness:

up quarks have charge $2/3$ and strangeness $0$ ,

down quarks have charge $-1/3$ and strangeness $0$ ,

strange quarks have charge $-1/3$ and strangeness $-1$ .

6.30 From the point of view of the strong nuclear force, the electric charge and strangeness don't play an important role beyond being conserved quantities. They don't tell you how strong the strong force is. For example, electric charge tells you about the strength of electromagnetic interactions, not strong interactions. So from the point of view of the strong force, these three quarks are more-or-less the same.

7.10 In quantum mechanics, we don't just have three discrete flavours of quarks: those are just three possible states of a quark, and we're allowed to take complex linear combinations of states. So the space of possible states of a quark is $\mathbf{C}^{3}$ : the states corresponding to up, down and strange quarks are just a basis of this vector space.

8.25 When you combine particles in quantum mechanics, the space of states of the combination is the tensor product of the state spaces for the individual particles, so a configuration of three quarks has state space $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}.$

9.00 The fact that the strong force "doesn't know the difference" between the three quarks means that there is some symmetry of $\mathbf{C}^{3}$ which allows you to switch between up, down and strange quarks. The proposal was that this symmetry should be the standard action of $SU(3)$ on $\mathbf{C}^{3}$ .

Remark:

This is only an approximate symmetry, useful for thinking about how particles interact under the strong force. You can't really switch the nature of particles like this because they have different masses and charges and you'd violate many conservation laws. But if you assume that you can switch particles like this, the conclusions you draw will be approximately valid for considerations involving the strong force, e.g. if you're trying to understand decay modes of these particles.

9.50 Although $SU(3)$ makes all quarks look alike, it doesn't make all combinations of three quarks look alike. This is because:

in the standard representation there are no subrepresentations, you can rotate any state (direction in $\mathbf{C}^{3}$ ) to any other state.

the representation $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}$ decomposes into subrepresentations. If you start in one of these subrepresentations and act using $SU(3)$ you never leave the subrepresentation. So there's a potentially measurable difference between states in the $\Gamma_{3,0}$ subrepresentation and the states in one of the $\Gamma_{1,1}$ subrepresentations, for example.

Example:

The trivial 1-dimensional subrepresentation is spanned by the unique completely antisymmetric combination of quarks. If we write our basis as $u, d, s$ (for up, down, strange) then this means $u\otimes d\otimes s-d\otimes u\otimes s+d\otimes s\otimes u-u\otimes s\otimes d% +s\otimes u\otimes d-s\otimes d\otimes u.$ There's no way to rotate between this combination of quarks and a symmetric combination like $u\otimes u\otimes u\in\Gamma_{3,0}$ without the strong force knowing about it.

12.15 In other words, the strong force can tell the particles in the spin $3/2$ group (the baryon decuplet) apart from the particles in the spin $1/2$ group (the baryon octet).

Remark:

12.50 One thing which looks a bit odd is that there are two octets in the decomposition of $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}$ , but we only have one baryon octet. This is because we have been a bit careless in our analysis and have neglected spin from our considerations.

Remark:

13.35 There are other particles which aren't baryons. For example, there are mesons (medium weight particles). These have a similar description: a meson is a combination of a quark and an antiquark. Antiquarks transform according to the dual of the standard representation, which we'll discuss next.

This use of representation theory to explain the patterns occurring in the classification of hadrons is one of my favourite pieces of applied mathematics: it uses some really nontrivial mathematics to give a staggeringly simple explanation of patterns which are otherwise bewildering.

Further watching...

Strangeness minus 3 - a BBC Horizon documentary about the prediction and discovery of the Omega minus particle. Featuring interviews and discussion with Gell-Mann, Ne'eman and Feynman.