In fact, little h equals little g_0.
sl(2,C) subalgebras, 1
Review of SU(3)
When we studied the representation theory of G = SU(3) (or of its Lie algebra little g equals little s l 3 C, one of the key pictures we studied was the root diagram: the weight diagram of its adjoint representation. This was a hexagonal configuration of roots at L_i minus L_j with i and j in the set 1, 2, 3, i not equal to j.
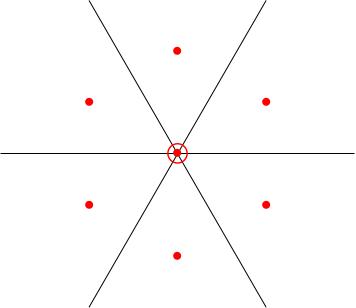
We'll write little g (L_i minus L_j) for the root space corresponding to the root L_i minus L_j and little g_0 for the weight space corresponding to 0. Recall that little g_0 is spanned by H_{1 3} and H_[2 3}, in other words, its the space of diagonal matrices theta_1, theta_2, minus theta_1 minus theta_2 where theta_1 and theta_2 run over the complex numbers.
This Lie algebra has the nice property that if we pick one root L_i minus L_j and its opposite root L_j minus L_i), and we pick generators E_{i j} in little g (L_i minus L_j) and E_{j i} in little g (L_j minus L_i) then the three elements E_{i j}, E_{j i} and H_{i j} equals E_{i j} bracket E_{j i} span a Lie subalgebra isomorphic to little s l 2 C. Our study of the structure of little s l 3 C representations used the three little s l 2 C subalgebras we obtained this way: for example, it gave us the Weyl symmetry group. This will generalise.
Roots in general
The setup
Suppose K is a compact matrix group with Lie algebra little k. Let's write little g for the complexification little k tensor C. Inside K we have a maximal torus T with Lie algebra little t. Let's write little h for little t tensor C, inside little g. The adjoint representation is a map big Ad from big K to big G L of little k, defined by g maps to big Ad_g, which sends X to g X g inverse. The same formula defines a complex representation, also written big Ad from big K to big G L of little g, if we allow X to live in little g. By taking the derivative we get the Lie algebra representation little ad from little k to little g l of little g and its complexification little ad superscript C from little g to little g l of little g.
The root diagram
Because we have a maximal torus, we get a weight space decomposition little g splits as a direct sum of weight spaces little g alpha where little g alpha equals the set of X in little g such that little ad_H of X equals alpha of H times X for all H in little h. The direct sum is happening over a finite set of weights. Which weights occur in this direct sum?
-
alpha equals zero occurs, in other words little g_0 is nonzero. This is because little h is an abelian Lie algebra, so little ad_H of H prime equals zero for all H and H prime in little h. Therefore little h is contained in little g_0 (just like in the SU(3) example).
Suppose Z is in little g_0, i.e. Z is in little g and little ad_H of Z equals 0 for all H in little H. Then H bracket Z equals 0 for all H in little h. In particular, H bracket Z equals 0 for all H in little t inside little h.
Let's write Z = X + i Y where X and Y live in little k (so they are the real and imaginary parts of Z). Then 0 equals H bracket Z, which equals H bracket X plus i times H bracket Y for all H in little t, therefore both real and imaginary parts must vanish, and H bracket X equals H bracket Y equals 0. This means that X and Y in little k commute with all elements in little t.
If either X or Y is not contained in little t then either little t direct sum the line spanned by X or little t direct sum the line spanned by Y will be an abelian subalgebra little t prime strictly containing little t. Then the topological closure of exp of little t prime is a torus strictly containing T, which contradicts the assumption that T is a maximal torus.
Which other weights occur?
Any nonzero weight of the adjoint representation is called a
Action of root vectors
-
If X is in the root space little g alpha and Y is in the root space little g beta then X bracket Y is in the root space little g alpha plus beta. (We won't prove this: it's an exercise, very similar to the corresponding results for little s l 2 C and little s l 3 C, like "X moves things to the right and Y moves things to the left".)
-
If X is in the root space little g alpha and Y is in the root space little g beta then K(X, Y) = 0 unless alpha plus beta equals zero.
-
If little g is semisimple then alpha is a root if and only if minus alpha is a root.
(2). Pick a basis of little g consisting of root vectors. We'll compute the matrix of little ad_X times little ad_Y with respect to this basis and then take the trace to find K(X, Y). Suppose Z in little g gamma is one of our basis vectors. Where does Z go under little ad_X times little ad_Y? By part (a), little ad_X times little ad_Y applied to Z equals X bracket (Y bracket Z), which lives in little g alpha plus beta plus gamma.
Let's write little ad_X times little ad_Y as a block matrix with respect to the splitting into weight spaces (i.e. the i,j block in the matrix is the matrix of the map little g lambda_i to little g lambda_j).
The diagonal blocks encode the maps little g lambda to little g lambda. But if alpha plus beta is nonzero then little ad_X times little ad_Y sends little g lambda to little g lambda plus alpha plus beta, which is not equal to little g lambda, so there are no nonzero diagonal blocks if alpha plus beta is nonzero. Therefore the trace of this matrix vanishes and K(X, Y) = 0.
(3) If little g is semisimple then the Killing form is nondegenerate, so for all nonzero X there exists Y such that K of X, y is nonzero. In particular, if X is in the root space little g alpha then there exists Y such that K of X, Y is nonzero.
Take the components of Y equals sum over weights lambda of Y lambda with respect to the weight space splitting. Then K of X, Y lambda equals zero unless lambda equals minus alpha. Therefore, if K of X, Y is nonzero, we must have that the minus alpha component of Y is nonzero, so little g minus alpha is nonzero and minus alpha is a root.
The trick for extracting the little s l 2 C subalgebras will be the following theorem which we'll prove next time.
If X in the root space little g alpha, Y in the root space little g minus alpha are nonzero then X, Y and H equals X bracket Y will span a subalgebra isomorphic to little s l 2 C.
Pre-class exercise
True or false: If we use a sub-maximal torus, is it still true that little h equals little g_0? If so, why? If not, what do we get instead?