Dihedral angles

Statement of result

Explanation

0.15 By the angle between two hyperplanes, I mean the following:

• take the unit vectors $v$ and $w$ orthogonal to these hyperplanes,

• take the smallest angle $\varphi$ such that $\cos \varphi =v\cdot w$ .

1.05 In a root system, the vectors orthogonal to the root hyperplanes are the (simple) roots, so we are really interested in $\alpha \cdot \beta$ where $\alpha$ and $\beta$ are roots. Recall that the dot product is the Killing form.

Proof

1.30 Since we're in a root system, if $\alpha$ and $\beta$ are roots then $P_{\alpha }(\beta )=\frac{1}{2}{n}_{\beta \alpha }\alpha$ for some $n_{\beta \alpha }\in 𝐙$ , where $P_{\alpha }(\beta )$ is the orthogonal projection of $\beta$ onto the line through $\alpha$ .

Example:

2.00 In the $SU(3)$ root system shown below, the projection of $\beta$ to the line through $\alpha$ gives $-\alpha /2$ .

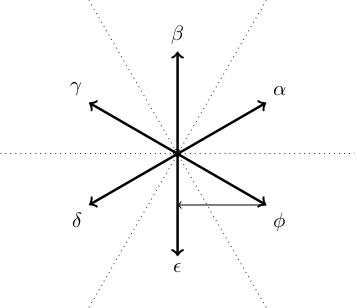
2.50 By Euclidean geometry, we have $$P_{\alpha }(\beta )=\frac{\alpha \cdot \beta }{\alpha \cdot \alpha }\alpha .$$

3.35 This means that $$n_{\beta \alpha }=\frac{2\alpha \cdot \beta }{\alpha \cdot \alpha }.$$ We also have $$n_{\alpha \beta }=\frac{2\alpha \cdot \beta }{\beta \cdot \beta },$$ so $$n_{\beta \alpha }{n}_{\alpha \beta }=\frac{4{(\alpha \cdot \beta )}^2}{(\alpha \cdot \alpha )(\beta \cdot \beta )}=4{\cos }^2(\varphi ),$$

4.30 where $\varphi$ is the angle between the roots.

4.50 We have because the roots are not collinear, so $$n_{\alpha \beta }{n}_{\beta \alpha }=4{\cos }^2\varphi \in \{0,1,2,3\}$$ because it's an integer between 0 and 4.

6.05 These possibilities give $\varphi =\{\begin{array}{cc}90\hfill & \\ 60\hfill & \\ 45\hfill & \\ 30\hfill & \end{array}$ degrees.