Classification of root systems, 2

Classification of root systems, continued

Dihedral angles

Lemma:

0.00 The dihedral angle between two of the root hyperplanes in a root system can be $90$ , $60$ , $45$ or $30$ degrees and nothing else.

The proof of this lemma will appear in another video. Let's see some examples of root systems which have these dihedral angles.

Examples

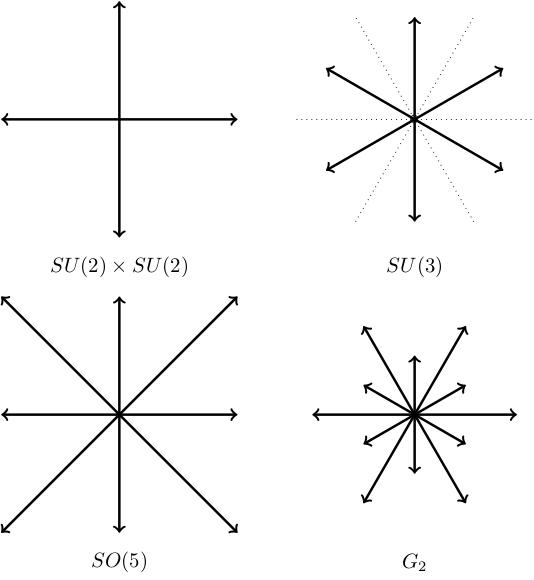
Root diagrams of SU(2) times SU(2), SU(3), SO(5) and G_2

1.00 These are the root systems of $SU(2)\times SU(2)$ , $SU(3)$ , $SO(5)$ and $G_{2}$ respectively.

For $SU(2)\times SU(2)$ , the orthogonal projection of any root onto any of the other root lines gives zero (as the roots are all orthogonal to one another). Therefore $n_{\beta\alpha}=0$ for all pairs of non-collinear roots $\alpha$ and $\beta$ . The angles between the mirrors are $90$ degrees.

2.05 The example of $SU(3)$ we've studied in some detail already. The dihedral angle is $60$ degrees.

The example of $SO(5)$ has some long roots and some short roots. For example, if we project onto the line through a short root then we get $n_{\beta\alpha}=-1,0,1$ . If we project onto a long root, we get $n_{\beta\alpha}=-1/2,0,1/2$ . The minimal dihedral angle appearing here is 45 degrees.

The roots of SO(5) projecting to half-integer multiples of one another

3.40 The final example comes from a group called $G_{2}$ . This is one of the few groups we haven't met. There are six short roots and six long roots. The angle between neighbouring roots is $30$ degrees. If you project from a short root $\beta$ to a long root $\alpha$ you end up halfway to the long root (so $n_{\beta\alpha}=\pm 1/2$ ) and if you project from the long to the short root you end up $3/2$ of the way along the root line (so $n_{\alpha\beta}=\pm 3/2$ ).

The roots of G_2 projecting to half-integer multiples of one another

Remark:

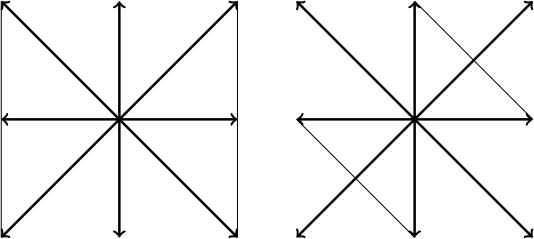
4.30 It will turn out that these four are the only 2-dimensional root systems.

Dynkin diagrams

4.45 Drawing pictures in 2-d and making models in 3-d is all very well, but what about root systems in higher dimensions? It turns out there's a very efficient way of encoding these diagrams using a graph called a Dynkin diagram or Coxeter-Dynkin diagram.

Definition:

5.20 Pick your favourite Weyl chamber. The boundary is a collection of $n$ mirrors corresponding to simple roots. We draw a dot for each mirror. We connect the dots with:

no edges if the dihedral angle is $90$ degrees,
one edge if the dihedral angle is $60$ degrees,
two edges if the dihedral angle is $45$ degrees,
three edges if the dihedral angle is $30$ degrees.

7.00 We further decorate the diagram with arrows on edges going from the dot corresponding to a short root to the dot corresponding to a long root.

Examples

Example:

7.30 For $SU(2)\times SU(2)$ , there are two mirrors at $90$ degrees, so the Dynkin diagram is just two dots, no edges.

Dynkin diagram of SU(2) times SU(2): two dots, no edges

Example:

For $SU(3)$ , the Weyl chamber is cut out by two mirrors at $60$ degrees to one another, so the Dynkin diagram is two dots connected by an edge.

Dynkin diagram of SU(3): two dots joined by an edge

Example:

8.00 For $SO(5)$ , the Weyl chamber is cut out by two mirrors at $45$ degrees. The Dynkin diagram is therefore two dots connected by two edges; the edges have arrows pointing from the mirror corresponding to the short root to the mirror corresponding to the long root (in this case, the diagram is symmetric, so it doesn't matter which direction we draw the arrows).

Dynkin diagram of SO(5): two dots joined by double edge with arrows

Example:

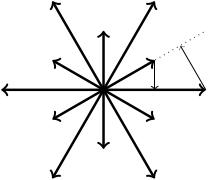
8.45 For $G_{2}$ , the Weyl chamber is cut out by two mirrors at $30$ degrees to one another. The Dynkin diagram is therefore two dots with three edges between them (and arrows pointing from the short roots to the long roots).

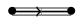
Dynkin diagram of G_2: two dots joined by triple edge with arrows

Example:

9.45 The 3-dimensional example we saw at the end of the last video had three mirrors making pairwise angles $60$ , $60$ and $90$ with one another. The Dynkin diagram is therefore three dots in a line, with single edges connecting the first to second and second to third dots.

Dynkin diagram of SU(4): three dots in a chain

Classification theorem

Theorem:

10.25 If $R$ is the root system of a compact semisimple Lie group then the Dynkin diagram of $R$ is a disjoint union of diagrams from the following list. (The diagrams on the list are connected; disjoint unions of Dynkin diagrams correspond to taking the product of the corresponding Lie algebras).

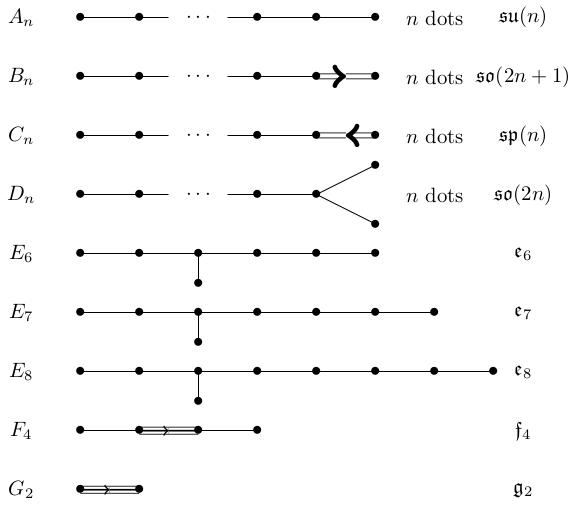
Dynkin diagrams of types A_n, B_n, C_n, D_n, E_6, E_7, E_8, F_4 and G_2. See text below for descriptions of these and the Lie algebras to which they correspond

Remark:

11.20 This is four infinite families of Dynkin diagrams $A_{n},B_{n},C_{n},D_{n}$ and five exceptional cases $E_{6},E_{7},E_{8},F_{4},G_{2}$ . The four infinite families were known classically; the exceptional groups were discovered by people trying to classify them. They are hard to construct.

Remarks

Remark:

12.05 Remember that this is a classification of semisimple Lie algebras up to isomorphism: it's possible to have different groups with the same Lie algebra and hence the same Dynkin diagram.

Example:

12.20 The first infinite family is $A_{n}$ . The subscript tells you the number of dots. These Dynkin diagrams are just chains of $n$ dots, the first connected to the second, second to the third etc by single edges. These are the Dynkin diagrams of $SU(n+1)$ .

Example:

13.05 The second infinite family is $B_{n}$ . These are the Dynkin diagrams of the odd-dimensional rotation groups $SO(2n+1)$ . The diagram is similar to $A_{n}$ except that the final two dots in the chain are connected by a double arrow pointing from vertex $n-1$ to vertex $n$ , so the final dot corresponds to a longer simple root.

Example:

13.30 The family $C_{n}$ is very similar except that the arrow goes the other way. These correspond to a family of groups called the symplectic groups $Sp(n)$ which we haven't discussed.

Example:

13.45 The family $D_{n}$ has a chain of $n-2$ dots with two further dots sprouting off the last dot in the chain. All edges are single edges. This is the Dynkin diagram of $SO(2n)$ (even-dimensional rotation group).

Example:

14.15 The $E_{6},E_{7},E_{8}$ graphs are respectively $5,6,7$ dots in a chain with one dot coming off the third dot (all edges single). This is not an infinite family: for example, the obvious thing you'd call an $E_{9}$ diagram doesn't correspond to a root system.

14.45 The $F_{4}$ diagram has four dots connected 1 to 2, 2 to 3 and 3 to 4 with 2 to 3 being a double arrow. $G_{2}$ has two dots connected by a triple arrow.

Remark:

15.00 It's quite surprising that we've been studying this big class of groups, but aside from one infinite family (symplectic groups) and five exceptional cases we'd never have dreamed of by ourselves, we're already familiar with all the examples.

Remark:

15.25 The Dynkin diagram is an amazingly economical way of encoding information. For example, the $E_{8}$ diagram is a complete recipe for building a configuration of eight 7-dimensional mirrors in 8-dimensional Euclidean space.

In what remains of the course, we will fill in some of the details of the proof of this theorem and the earlier lemmas.

Pre-class questions

Exercise:

Just by looking at the root diagrams, can you figure out the dimensions of the Lie algebras $\mathfrak{so}(5)$ and $\mathfrak{g}_{2}$ ?

Exercise:

Sketch the (3-dimensional) root system corresponding to your choice of Dynkin diagram from amongst: $A_{3}$ , $B_{3}$ , $C_{3}$ and $D_{3}$ .