Optional: Matrix norms

Matrix norms

0.00 We defined $\exp(A)=\sum_{n=0}^{\infty}\frac{1}{n!}A^{n}$ , $A^{0}=I$ , and claimed that it converges. What does it mean for a sequence of matrices to converge?

Definition:

0.30 A sequence $A_{k}$ of matrices converges to a matrix $A$ if, for all $\epsilon>0$ , there exists an $N$ such that $\lVert A_{k}-A\rVert<\epsilon$ whenever $k\geq N$ .

Here, $\lVert\cdot\rVert$ denotes a matrix norm, i.e. a way of measuring how "big" a matrix is.

Definition:

2.00 A matrix norm is any function $\lVert\cdot\rVert\colon\mathfrak{gl}(n,\mathbf{R})\to\mathbf{R}$ satisfying:

(triangle inequality) $\lVert A+B\rVert\leq\lVert A\rVert+\lVert B\rVert$ for all $A,B\in\mathfrak{gl}(n,\mathbf{R})$ ;
$\lVert\lambda A\rVert=|\lambda|\lVert A\rVert$ for all $A\in\mathfrak{gl}(n,\mathbf{R})$ and $\lambda\in\mathbf{R}$ ;
$\lVert A\rVert=0$ if and only if $A=0$ .

3.55 We will focus on two particular matrix norms.

L¹ norm

Definition:

The $L^{1}$ -norm of $A$ , is $\lVert A\rVert_{L^{1}}=\sum_{i,j}|A_{i,j}|$ . So a matrix is "big in the $L^{1}$ norm" if it has an entry with large absolute value.

If $\lVert A\rVert_{L^{1}}=0$ then $A_{ij}=0$ for all $i, j$ , so $A=0$ . If we rescale $A$ by $\lambda$ then all entries are scaled by $\lambda$ , so $\lVert\lambda A\rVert_{L^{1}}=|\lambda|\lVert A\rVert_{L^{1}}$ . The triangle inequality can be deduced by applying the triangle inequality for absolute values to each matrix entry.

Operator norm

Definition:

6.00 The operator norm of $A$ is defined to be $\lVert A\rVert_{op}=\max\{|Au|\ :\ u\in\mathbf{R}^{n},\ |u|=1\}$ where $|v|$ denotes the Euclidean length of $v\in\mathbf{R}^{n}$ , i.e. $|v|=\sqrt{v_{1}^{2}+\cdots+v_{n}^{2}}$ .

7.05 Another way to think of this is: you take the unit sphere in $\mathbf{R}^{n}$ , you apply $A$ to obtain an ellipsoid, and you take the furthest distance of a point on this ellipsoid from the origin.

Example:

Take $A=\begin{pmatrix}1&0\\ 0&2\end{pmatrix}$ . The $x$ -axis is fixed and the $y$ -axis is rescaled by a factor of 2. The unit circle therefore becomes an ellipse with height 2 and width 1. The furthest point from the origin is a distance 2 from the origin (either the north or south pole), so $\lVert A\rVert_{op}=2$ .

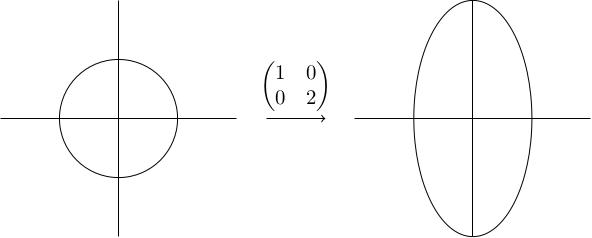
8.55 To see that the operator norm is a norm, note that:

If $\lVert A\rVert_{op}=0$ then all points on the ellipsoid image of the unit sphere are a distance 0 from the origin, so the image of the unit sphere is the origin. Therefore $A=0$ .
If you rescale $A$ by $\lambda$ then the lengths of the vectors $A u$ over which we are taking the maximum are rescaled by $|\lambda|$ , so $\lVert\lambda A\rVert_{op}=|\lambda|\lVert A\rVert_{op}$ .
9.30 To prove the triangle inequality, note that $|(A+B)u|=|Au+Bu|\leq|Au|+|Bu|\leq\lVert A\rVert_{op}+\lVert B\rVert_{op}$ . Since $\lVert A+B\rVert_{op}=\max\{|(A+B)u|\ :\ |u|=1\}$ , this shows $\lVert A+B\rVert_{op}\leq\lVert A\rVert_{op}+\lVert B\rVert_{op}$ .

Lipschitz equivalence

Lemma:

11.25 Any two matrix norms on $\mathfrak{gl}(n,\mathbf{R})$ are Lipschitz equivalent. For the two norms we've met so far, this means there exist constants $C_{1}$ , $C_{2}$ , $D_{1}$ , $D_{2}$ (independent of $M$ ) such that: $C_{1}\lVert A\rVert_{L^{1}}\leq\lVert A\rVert_{op}\leq C_{2}\lVert A\rVert_{L^% {1}}$ and $D_{1}\lVert A\rVert_{op}\leq\lVert A\rVert_{L^{1}}\leq D_{2}\lVert A\rVert_{op}.$

Remark:

13.15 These inequalities will be useful in the proof of convergence: sometimes it's easier to bound one or other, and this is telling us that if you can bound one then you can bound the other. It also tells us that the notion of convergence we defined (where we had implicitly picked a matrix norm) doesn't depend on which norm we picked.

14.40 We won't prove the lemma, but for those who are interested, it's true more generally that any two norms on a finite-dimensional vector space are Lipschitz equivalent. This fails for infinite-dimensional vector spaces, but we're working with $\mathfrak{gl}(n,\mathbf{R})$ which is $n^{2}$ -dimensional.

Properties of the operator norm

15.25 We will now prove some useful properties of the operator norm. Since we're only focusing on this norm, we will drop the subscript $o p$ and write it as $\lVert A\rVert$ .

Lemma:

For any vector $v\in\mathbf{R}^{n}$ , $|Av|\leq\lVert A\rVert|v|$ .
$\lVert AB\rVert\leq\lVert A\rVert\lVert B\rVert$ .
$\lVert A^{m}\rVert\leq\lVert A\rVert^{m}$ .

17.00 Write $v$ as $|v|u$ for some unit vector $u$ . Then $|Av|=|v||Au|\leq\lVert A\rVert|v|$ because $|Au|\leq\lVert A\rVert$ by definition of the operator norm.
18.45 Let $u$ be a unit vector. We have $|ABu|\leq\lVert A\rVert|Bu|\leq\lVert A\rVert\lVert B\rVert|u|=\lVert A\rVert% \lVert B\rVert$ using the first part of the lemma twice. This shows that the things we are maximising over to get $\lVert AB\rVert$ are all less than $\lVert A\rVert\lVert B\rVert$ , so $\lVert AB\rVert\leq\lVert A\rVert\lVert B\rVert$ .
19.50 Lastly, $\lVert A^{m}\rVert\leq\lVert A^{m-1}\rVert\lVert A\rVert\leq\cdots\leq\lVert A% \rVert^{m}$ using the previous part of the lemma inductively.

Matrix norms

L1 norm

Operator norm

Lipschitz equivalence

Properties of the operator norm

L¹ norm