4.02 Homotopy extension property (HEP)

Below the video you will find accompanying notes and some pre-class questions.

Previous video: 4.01 CW complexes.
Next video: 4.03 CW complexes and the HEP.
Index of all lectures.

Notes

(0.00) In this section, we will introduce the homotopy extension property, a useful tool for proving that different spaces are homotopy equivalent. For example, you can use it to prove that the \theta-graph and the figure 8 are homotopic ``just by squishing the middle bar of the \theta to a point'' (see image below), or the a sphere with a 1-cell attached (joining the North and South poles) is homotopy equivalent to a pinched torus ``just by squishing the 1-cell to the pinch point''.

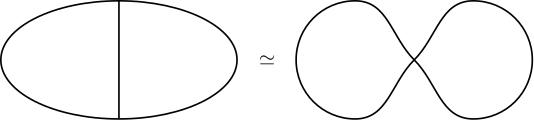
Homotopy extension property

(0.58) Given a space

$X$ and a subspace

$A$ , we say that the pair

$(X,A)$ has the homotopy extension property (HEP) if, for every continuous map

$F\colon X\to Y$ and every homotopy

$h\colon A\times[0,1]\to Y$ with

$h(x,0)=F(x)$ there exists a homotopy

$H\colon X\times[0,1]\to Y$ such that

$H(x,0)=F(x)$ and

$H|_{A\times[0,1]}=h$ .

(2.44) More colloquially, homotopies of functions defined on

$A$ extend to homotopies of functions defined on

$X$ (for given initial data).

(3.29) If

$(X,A)$ has the HEP and

$A$ is contractible, then

$X\simeq X/A$ , where

$X/A$ denotes the quotient space in which

$A$ is crushed to a single point.

(4.40) To prove that

$X\simeq X/A$ , we need to find continuous maps

$q\colon X\to X/A$ and

$g\colon X/A\to X$ such that

$g\circ q\simeq id_X$ and

$q\circ g\simeq id_{X/A}$ . The map

$q\colon X\to X/A$ will be the quotient map.

(5.20) Constructing the map $g\colon X/A\to X$ . The subspace $A$ is contractible, so there exists a point $a\in A$ and a homotopy $h_t\colon A\to A$ such that $h_0=id_A$ and $h_1(x)=a$ for all $x\in A$ . Since $A\subset X$ , we can think of this as a homotopy $h_t\colon A\to X$ .

(6.14) Using the HEP for the pair $(X,A)$ , we get a homotopy $H_t\colon X\to X$ such that $H_0=id_X$ and $(H_t)|_{A}=h_t$ . At $t=1$ , $h_1(A)=\{a\}$ and $(H_1)|_A=h_1$ , so $H_1(A)=\{a\}$ . Therefore $H_1=g\circ q$ for some continuous map $g\colon X/A\to X$ (in other words, $H_1$ descends to the quotient).

(7.57) The fact that $g$ is continuous follows from this section on continuous maps out of a quotient space (continuous maps from $X/\sim\to Y$ are just continuous maps $X\to Y$ which descend to the quotient). This map $g$ is going to be our homotopy inverse for $q$ .

(8.20) The map $g$ is a homotopy inverse for $q$ . We need to prove:

(9.00) $g\circ q\simeq id_X$ : This holds because $g\circ q=H_1\simeq H_0=id_X$ .
(9.22) $q\circ g\simeq id_{X/A}$ : Since $(H_t)|_{A}=h_t$ , the homotopy $q\circ H_t\colon X\to X/A$ has the property that $(q\circ H_t)(A)\subset q(h_t(A))\subset q(A)$ . Since $q(A)$ is a single point, this implies that $q\circ H_t$ factors as $\bar{H}_t\circ q$ for some continuous map $\bar{H}_t\colon X/A\to X/A$ (again, using our results on continuous maps out of a quotient space).
(11.22) We have $\bar{H}_0=id_{X/A}$ since $H_0=id_X$ . We want to show that $\bar{H}_1=q\circ g$ . We first notice that
$\bar{H}_1\circ q=q\circ H_1=q\circ (g\circ q)=(q\circ g)\circ q,$ which implies $\bar{H}_1=q\circ g$ if we can cancel the extra $q$ s on each side of the equation.
(12.34) We can cancel the $q$ s because $q$ is surjective (it's a quotient map) and surjective maps have right-inverses (so can be cancelled from the right).

(14.05) We will see in the next video that if

$X$ is a CW complex and

$A$ is a closed subcomplex then

$(X,A)$ has the HEP.

Pre-class questions

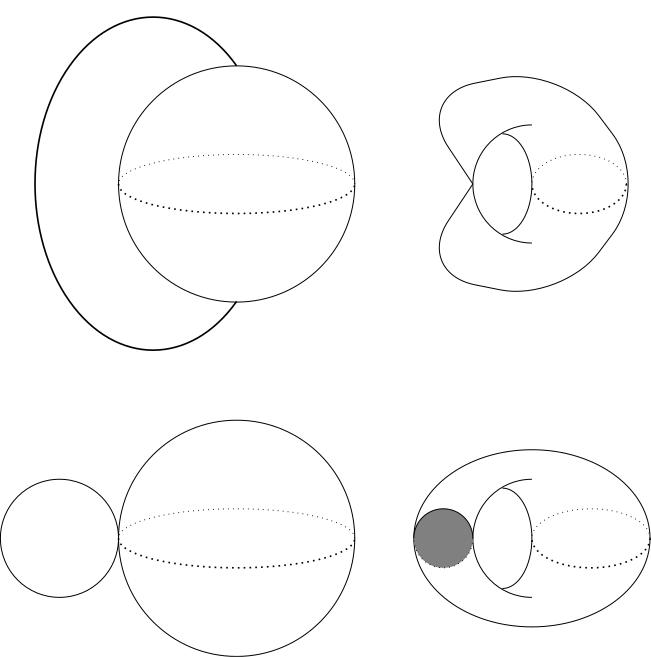
Assuming that you can use the HEP with impunity, which of the following spaces are homotopy equivalent to one another?

Navigation

Previous video: 4.01 CW complexes.
Next video: 4.03 CW complexes and the HEP.
Index of all lectures.