01. Matrices

Vectors in the plane

0.00 A vector is an arrow in the plane (later we'll deal with vectors in higher-dimensional spaces). We encode this arrow as a pair of numbers $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)$ . The number $x$ tells us how far to the right the arrow points; the number $y$ tells us how far upwards it points. If the arrow points to the left then $x$ is negative; if it points downwards then $y$ is negative.

1.00 Can you match up the vectors $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)$ with those in the diagram? (Some of the vectors are not depicted).

$$\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \end{array}\right),\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right),\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right),$$ $$\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill -1\hfill \\ \hfill -1\hfill \end{array}\right),\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \end{array}\right).$$

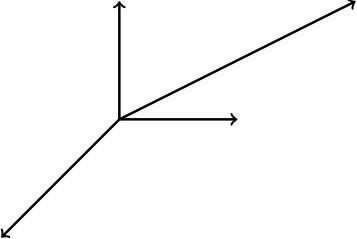
(answers at 2.08).

3.35 A lot of this module will focus on the interplay between algebra (like column vectors) and geometry (like arrows in the plane).

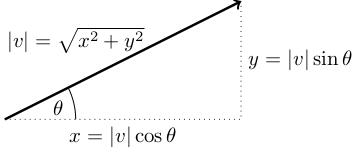
Suppose $v=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)$ is a vector. What is it's length? By Pythagoras's theorem, it's $\sqrt{x^2+y^2}$ . I'll write this as $|v|$ , which you can read out loud as "norm $v$ ". The angle that $v$ makes with the horizontal is $\theta =\arctan (y/x)$ (by trigonometry). If we want to write $x$ and $y$ in terms of $|v|$ and $\theta$ , we get (again, using trigonometry): $$x=|v|\cos \theta ,y=|v|\sin \theta .$$ So $v=\left(\begin{array}{c}\hfill |v|\cos \theta \hfill \\ \hfill |v|\sin \theta \hfill \end{array}\right)$ .

2-by-2 matrices

6.15 What happens if I rotate $v$ by an angle $\varphi$ anticlockwise? We get a new vector $w$ , which we can express in terms of $v$ and $\varphi$ .

Rotation preserves lengths, so $|w|=|v|$ .

8.07 The angle that $w$ makes with the horizontal is $\theta +\varphi$ . Therefore $$w=\left(\begin{array}{c}\hfill |v|\cos (\theta +\varphi )\hfill \\ \hfill |v|\sin (\theta +\varphi )\hfill \end{array}\right).$$

9.20 We can expand this using the trigonometric addition formulae: $$w=\left(\begin{array}{c}\hfill |v|\cos (\theta +\varphi )\hfill \\ \hfill |v|\sin (\theta +\varphi )\hfill \end{array}\right)=\left(\begin{array}{c}\hfill |v|\cos \theta \cos \varphi -|v|\sin \theta \sin \varphi \hfill \\ \hfill |v|\sin \theta \cos \varphi +|v|\cos \theta \sin \varphi \hfill \end{array}\right).$$

10.27 Using $x=|v|\cos \theta$ and $y=|v|\sin \theta$ , we get $$w=\left(\begin{array}{c}\hfill x\cos \varphi -y\sin \varphi \hfill \\ \hfill x\sin \varphi +y\cos \varphi \hfill \end{array}\right).$$

11.34 This expresses $w$ in terms of the original vector $v=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)$ and the angle $\varphi$ of rotation. We now invent a piece of notation which separates out the dependence of $w$ on $v$ from its dependence on $\varphi$ : we write You can just think of this as a shorthand for $\left(\begin{array}{c}\hfill x\cos \varphi -y\sin \varphi \hfill \\ \hfill x\sin \varphi +y\cos \varphi \hfill \end{array}\right)$ , keeping track of where all the coefficients sit.

13.00 More generally, given a 2-by-2 array of numbers and a vector $v=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)$ , we define the product This defines the action of a matrix on a vector. This notation completely separates out the rotation ($M$ ) from the vector we started with ($v$ ).

15.09 Now we don't have to limit ourselves to rotations: any matrix defines a geometric transformation of the plane. This is the transformation $$\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right)\mapsto \left(\begin{array}{c}\hfill ax+by\hfill \\ \hfill cx+dy\hfill \end{array}\right).$$ We'll see lots of examples in the next video (rotations, reflections, shears,...).

Mnemonic

16.34 How do you remember the formula for a matrix acting on a vector? The mnemonic I like is as follows. To get the first entry of $Mv$ , you ``multiply the top row of $M$ into $v$ '', that is you perform the multiplications $ax$ and $by$ (working across the top row of $M$ and down the column of $v$ ) and sum them.

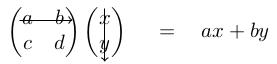
To get the second entry, you multiply the second row of $M$ into $v$ .

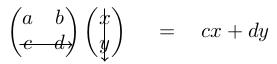
In the next video, we'll see lots of examples of transformations of the plane coming from 2-by-2 matrices.