01. Matrices

Vectors in the plane

0.00 A vector is an arrow in the plane (later we'll deal with vectors in higher-dimensional spaces). We encode this arrow as a pair of numbers x, y. The number x tells us how far to the right the arrow points; the number y tells us how far upwards it points. If the arrow points to the left then x is negative; if it points downwards then y is negative.

1.00 Can you match up the vectors x, y with those in the diagram? (Some of the vectors are not depicted).

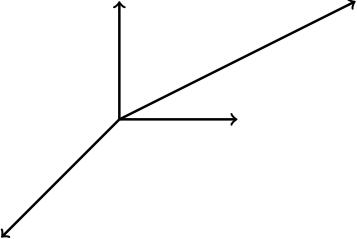
1, 2; 0, 1; 1, 1; 1, 0; minus 1, minus 1; 2, 1.

(answers at 2.08).

3.35 A lot of this module will focus on the interplay between algebra (like column vectors) and geometry (like arrows in the plane).

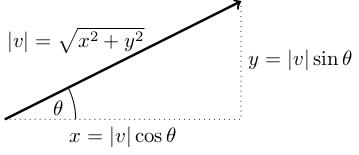
Suppose v equals x, y is a vector. What is it's length? By Pythagoras's theorem, it's square root of x squared plus y squared. I'll write this as norm v, which you can read out loud as "norm v". The angle that v makes with the horizontal is theta equals arctan (y over x) (by trigonometry). If we want to write x and y in terms of norm v and theta, we get (again, using trigonometry): x equals norm v cos theta, y equals norm v sine theta So v equals the vector norm v cos theta, norm v sine theta.

2-by-2 matrices

6.15 What happens if I rotate v by an angle phi anticlockwise? We get a new vector w, which we can express in terms of v and phi.

Rotation preserves lengths, so norm w equals norm v.

8.07 The angle that w makes with the horizontal is theta plus phi. Therefore w equals norm v cos (theta plus phi), norm v sine (theta plus phi).

9.20 We can expand this using the trigonometric addition formulae: w equals norm v cos theta plus phi, norm v sin theta plus phi, which equals norm v cos theta cos phi minus norm v sine theta sine phi, norm v sine theta cos phi plus norm v cos theta sine phi.

10.27 Using x equals norm v cos theta and y equals norm v sine theta, we get w equals x cos phi minus y sine phi, x sine phi plus y cos phi.

11.34 This expresses w in terms of the original vector v equals x, y and the angle phi of rotation. We now invent a piece of notation which separates out the dependence of w on v from its dependence on phi: we write w equals the 2-by-2 matrix cos phi, minus sine phi; sine phi, cos phi; times the vector x, y. You can just think of this as a shorthand for x cos phi minus y sine phi, x sine phi plus y cos phi., keeping track of where all the coefficients sit.

13.00 More generally, given a 2-by-2 array of numbers M equals a, b; c, d and a vector v equals x, y, we define the product M v equals a, b; c, d times x, y; equals a x plus b y, c x plus d y. This defines the action of a matrix on a vector. This notation completely separates out the rotation (M) from the vector we started with (v).

15.09 Now we don't have to limit ourselves to rotations: any matrix a, b; c, d defines a geometric transformation of the plane. This is the transformation x, y maps to a x plus b y, c x plus d y. We'll see lots of examples in the next video (rotations, reflections, shears,...).

Mnemonic

16.34 How do you remember the formula for a matrix acting on a vector? The mnemonic I like is as follows. To get the first entry of M v, you ``multiply the top row of M into v'', that is you perform the multiplications a x and b y (working across the top row of M and down the column of v) and sum them.

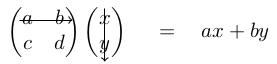
To get the second entry, you multiply the second row of M into v.

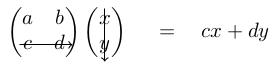
In the next video, we'll see lots of examples of transformations of the plane coming from 2-by-2 matrices.