02. Matrices: examples

02. Examples

Vectors in the plane

0.00 In the last video, we saw that a 2-by-2 matrix of numbers $\begin{pmatrix}a&b\\ c&d\end{pmatrix}$ defines a geometric transformation of the plane $\mathbf{R}^{2}$ : $\begin{pmatrix}x\\ y\end{pmatrix}\mapsto\begin{pmatrix}ax+by\\ cx+dy\end{pmatrix}.$

Remark:

Recall that $\mathbf{R}$ denotes the real number line. $\mathbf{R}^{2}$ denotes the 2-dimensional plane of all column vectors of height 2 (i.e. $\begin{pmatrix}x\\ y\end{pmatrix}$ ); $\mathbf{R}^{3}$ denotes the 3-dimensional space of all column vectors of height 3 (i.e. $\begin{pmatrix}x\\ y\\ z\end{pmatrix}$ ; and more generally, $\mathbf{R}^{n}$ denotes the $n$ -dimensional space of all column vectors of height $n$ (i.e. $\begin{pmatrix}x_{1}\\ x_{2}\\ \vdots\\ x_{n}\end{pmatrix}$ ).

1.52 Just as the coordinates $\begin{pmatrix}x\\ y\end{pmatrix}$ encode points in the plane, we should think of the matrix $\begin{pmatrix}a&b\\ c&d\end{pmatrix}$ as encoding a transformation of the plane. In this lecture, we will take a range of examples and see what the corresponding transformation looks like.

Example 1

2.30 Let $M=\begin{pmatrix}1&0\\ 0&0\end{pmatrix}$ . If I apply $M$ to $v=\begin{pmatrix}x\\ y\end{pmatrix}$ then I get $Mv=\begin{pmatrix}1&0\\ 0&0\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}x\\ 0\end{pmatrix}.$ This takes $v$ to the point on the $x$ -axis with the same $x$ -coordinate, so $M$ represents a vertical projection map to the $x$ -axis.

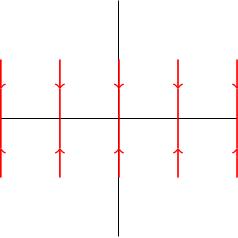
Example 2

4.05 Consider the action of $\begin{pmatrix}1&0\\ 0&1\end{pmatrix}$ . This sends $\begin{pmatrix}x\\ y\end{pmatrix}$ to $\begin{pmatrix}x\\ y\end{pmatrix}$ ; this transformation leaves everything as it was: it is called the identity transformation. We call this matrix the identity matrix, and we often write this matrix as $I$ ; it plays the role of the number $1$ in the algebra of matrices.

Useful lemma

Lemma:

5.35 Let $M=\begin{pmatrix}a&b\\ c&d\end{pmatrix}$ , let $e_{1}=\begin{pmatrix}1\\ 0\end{pmatrix}$ and $e_{2}=\begin{pmatrix}0\\ 1\end{pmatrix}$ . Then

$Me_{1}$ is the first column of $M$ , i.e. $\begin{pmatrix}a\\ c\end{pmatrix}$ .
$Me_{2}$ is the second column of $M$ , i.e. $\begin{pmatrix}b\\ d\end{pmatrix}$ .

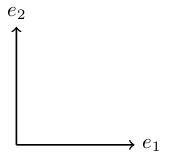
We'll call $e_{1},e_{2}$ basis vectors, which basically means that any other vector can be written as a combination of $e_{1}$ and $e_{2}$ in a unique way. More on this in MATH220.

We'll just check it for $Me_{1}$ : $Me_{1}=\begin{pmatrix}a&b\\ c&d\end{pmatrix}\begin{pmatrix}1\\ 0\end{pmatrix}=\begin{pmatrix}a+0\\ c+0\end{pmatrix}=\begin{pmatrix}a\\ c\end{pmatrix}.$ The calculation for $Me_{2}$ is similar.

Example 3

8.38 Take $M=\begin{pmatrix}0&1\\ 1&0\end{pmatrix}$ .

Where does $e_{1}$ go? It goes to the first column of $M$ , which is $e_{2}$ .
Where does $e_{2}$ go? It goes to the second column of $M$ , which is $e_{1}$ .

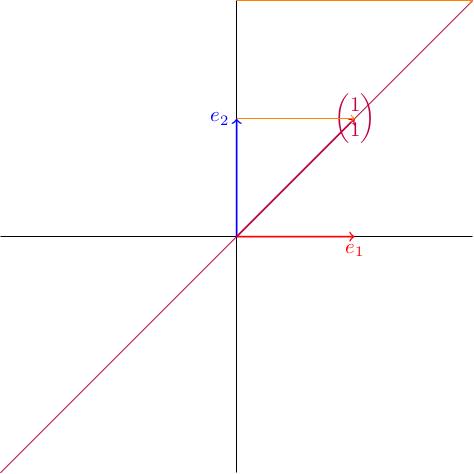
So $e_{1}$ and $e_{2}$ get switched. This corresponds to a reflection in the line $y=x$ :

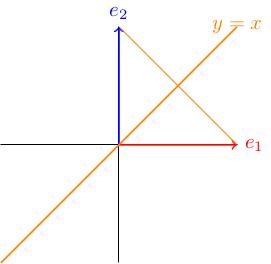
10.12 Let's check that the line $y=x$ is indeed fixed by the action of $M$ . The vectors $\begin{pmatrix}x\\ x\end{pmatrix}$ (and only these ones) lie on this line, so let's compute: $M\begin{pmatrix}x\\ x\end{pmatrix}=\begin{pmatrix}x\\ x\end{pmatrix},$ which indeed tells us that the points on the line $y=x$ are fixed.

Example 4

11.24 Take $M=\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}$ .

Where does $e_{1}$ go? It goes to the first column of $M$ , which is $e_{2}$ .
Where does $e_{2}$ go? It goes to the second column of $M$ , which is $-e_{1}$ .

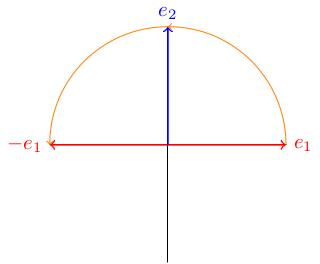
We see that this looks like a 90 degree ( $\pi/2$ radian) rotation. This makes sense, because the matrix $\begin{pmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}$ for a rotation by an angle $\theta$ specialises to $M$ when $\theta=\pi/2$ , because $\cos(\pi/2)=0$ and $\sin(\pi/2)=1$ .

Example 5

14.00 Take $M=\begin{pmatrix}1&1\\ 0&1\end{pmatrix}$ . We have

$e_{1}\mapsto e_{1}$ ,
$e_{2}\mapsto\begin{pmatrix}1\\ 1\end{pmatrix}$ .

So $e_{1}$ is fixed, but $e_{2}$ is slanted over in the $x$ -direction. In fact, the whole $y$ -axis gets slanted in the $x$ -direction, for example if we compute $M\begin{pmatrix}0\\ 2\end{pmatrix}$ we get $\begin{pmatrix}2\\ 2\end{pmatrix}$

Example 6

As one final example, we'll take $M=\begin{pmatrix}-3&16\\ -1&5\end{pmatrix}$ . What on earth does this correspond to? I claim that it corresponds to a shear in a different direction. How can we find the fixed direction?

18.00 If $v=\begin{pmatrix}x\\ y\end{pmatrix}$ points in the direction fixed by $M$ then $v=Mv$ (that's what it means to be fixed). Therefore $\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}-3&16\\ -1&5\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}.$

18.57 In other words, the first entries of $v$ and $M v$ must coincide, and so must the second entries. This gives us a pair of linear simultaneous equations: $x=-3x+16y,\qquad y=-x+5y.$ These are both equivalent to $y=x/4$ , so the line $y=x/4$ is fixed.

Remark:

20.50 Not all matrices have fixed directions, but if they do then this method will find it.

Outlook

In the next video, we will take a look at bigger matrices and higher-dimensional spaces.