In the last video, we saw that a 2-by-2 matrix of numbers a, b; c, d defines a geometric transformation of the plane R 2: x, y mapsto a x plus b y, c x plus d y.
Recall that R denotes the real number line. R 2 denotes the 2-dimensional plane of all column vectors of height 2 (i.e. x, y); R 3 denotes the 3-dimensional space of all column vectors of height 3 (i.e. x, y, z; and more generally, R n denotes the n-dimensional space of all column vectors of height n (i.e. x_1, x_2, dot dot dot, x_n).
Just as the coordinates x, y encode points in the plane, we should think of the matrix a, b; c, d as encoding a transformation of the plane. In this lecture, we will take a range of examples and see what the corresponding transformation looks like.
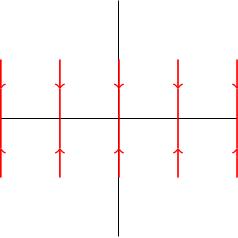
Let M be the 2-by-2 matrix 1, 0; 0, 0. If I apply M to the vector v equals x, y then I get M v equals 1, 0; 0, 0 times x, y, which equals x, 0. This takes v to the point on the x-axis with the same x-coordinate, so M represents a vertical projection map to the x-axis.
Consider the action of the 2-by-2 matrix 1, 0; 0, 1. This sends x, y to x, y; this transformation leaves everything as it was: it is called the identity transformation. We call this matrix the identity matrix, and we often write this matrix as I; it plays the role of the number 1 in the algebra of matrices.
Let M be the 2-by-2 matrix a, b; c, d, let e_1 be the vector 1, 0 and e_2 be the vector 0, 1. Then
M e_1 is the first column of M, i.e. a, c.
M e_2 is the second column of M, i.e. b, d.
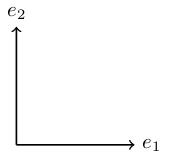
We'll call e_1, e_2 basis vectors, which basically means that any other vector can be written as a combination of e_1 and e_2 in a unique way. More on this in MATH220.
We'll just check it for M e_1: M e_1 equals a, b; c, d times 1, 0, which equals a plus 0, c plus 0, which equals a, c The calculation for M e_2 is similar.
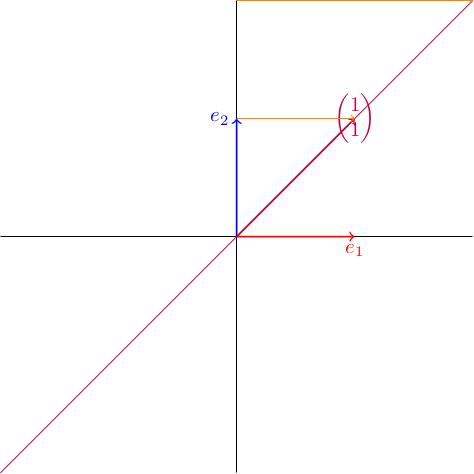
Take M to be the 2-by-2 matrix 0, 1; 1, 0.
Where does e_1 go? It goes to the first column of M, which is e_2.
Where does e_2 go? It goes to the second column of M, which is e_1.
So e_1 and e_2 get switched. This corresponds to a reflection in the line y = x:
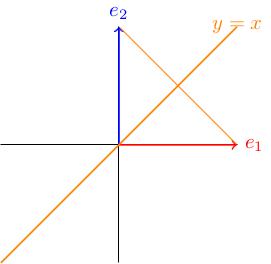
Let's check that the line y = x is indeed fixed by the action of M. The vectors x, x (and only these ones) lie on this line, so let's compute: M times x, x equals x, x which indeed tells us that the points on the line y = x are fixed.
Take M to be the 2-by-2 matrix 0, minus 1; 1, 0.
Where does e_1 go? It goes to the first column of M, which is e_2.
Where does e_2 go? It goes to the second column of M, which is minus e_1.
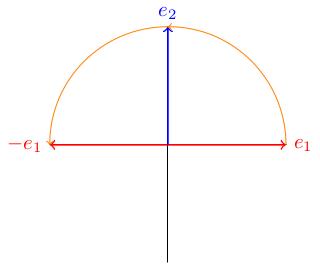
We see that this looks like a 90 degree (pi over 2 radian) rotation. This makes sense, because the matrix cos theta, minus sine theta, sine theta, cos theta for a rotation by an angle theta specialises to M when theta equals pi over 2, because cos of pi over 2 equals 0 and sine of pi over 2 equals 1.
Take M to be the 2-by-2 matrix 1, 1; 0, 1. We have
e_1 maps to e_1,
e_2 maps to 1, 1.
So e_1 is fixed, but e_2 is slanted over in the x-direction. In fact, the whole y-axis gets slanted in the x-direction, for example if we compute M times 0, 2 we get 2, 2
As one final example, we'll take M to be the 2-by-2 matrix minus 3, 16; minus 1, 5. What on earth does this correspond to? I claim that it corresponds to a shear in a different direction. How can we find the fixed direction?
If v equals x, y points in the direction fixed by M then v = M v (that's what it means to be fixed). Therefore x, y equals minus 3, 16; minus 1, 5 times x, y
In other words, the first entries of v and M v must coincide, and so must the second entries. This gives us a pair of linear simultaneous equations: x equals minus 3 times x plus 16 y; y equals minus x plus 5 y. These are both equivalent to y equals x over 4, so the line y equals x over 4 is fixed.
Not all matrices have fixed directions, but if they do then this method will find it.
In the next video, we will take a look at bigger matrices and higher-dimensional spaces.