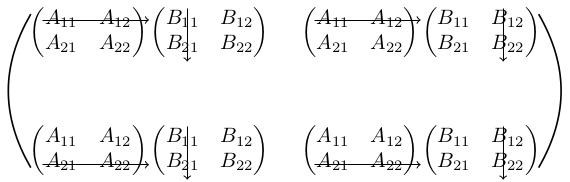04. Matrix multiplication, 1

Composing transformations

0.00 Recall that a 2-by-2 matrix defines for us a transformation of the plane. Suppose we are given two matrices $A=\begin{pmatrix}A_{11}&A_{12}\\ A_{21}&A_{22}\end{pmatrix},\qquad B=\begin{pmatrix}B_{11}&B_{12}\\ B_{21}&B_{22}\end{pmatrix}.$ They each define a transformation of the plane. What happens if we first do the transformation associated to $B$ , and then do the transformation associated to $A$ ?

2.15 We get a new transformation associated to a new matrix, which we call $A B$ . $A(B(v))=\begin{pmatrix}A_{11}&A_{12}\\ A_{21}&A_{22}\end{pmatrix}\begin{pmatrix}B_{11}&B_{12}\\ B_{21}&B_{22}\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}$ $=\begin{pmatrix}A_{11}&A_{12}\\ A_{21}&A_{22}\end{pmatrix}\begin{pmatrix}B_{11}x+B_{12}y\\ B_{21}x+B_{22}y\end{pmatrix}$ $=\begin{pmatrix}A_{11}B_{11}x+A_{11}B_{12}y+A_{12}B_{21}x+A_{12}B_{22}y\\ A_{21}B_{11}x+A_{21}B_{12}y+A_{22}B_{21}x+A_{22}B_{22}y\end{pmatrix}$ $=\begin{pmatrix}A_{11}B_{11}+A_{12}B_{21}&A_{11}B_{12}+A_{12}B_{22}\\ A_{21}B_{11}+A_{22}B_{21}&A_{21}B_{12}+A_{22}B_{22}\end{pmatrix}\begin{pmatrix% }x\\ y\end{pmatrix}$ $=:(AB)v$

Definition:

8.25 Given matrices $A=\begin{pmatrix}A_{11}&A_{12}\\ A_{21}&A_{22}\end{pmatrix}$ , and $B=\begin{pmatrix}B_{11}&B_{12}\\ B_{21}&B_{22}\end{pmatrix}$ , we define the matrix product $AB=\begin{pmatrix}A_{11}B_{11}+A_{12}B_{21}&A_{11}B_{12}+A_{12}B_{22}\\ A_{21}B_{11}+A_{22}B_{21}&A_{21}B_{12}+A_{22}B_{22}\end{pmatrix}.$

Mnemonic

9.08 How on earth can we remember this formula? Here is a mnemonic. Just like when we act on a vector using a matrix, we can think of the entries of $A B$ as "multiplying a row of $A$ into a column of $B$ ". More specifically, to get the $i j$ th entry of $A B$ (i.e. $i$ th row and $j$ th column) we multiply the $i$ th row of $A$ into the $j$ th column of $B$ :