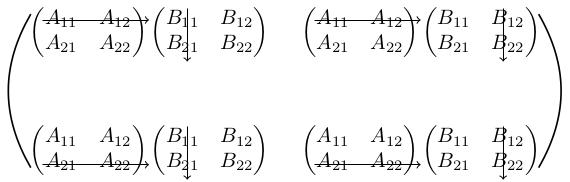Recall that a 2-by-2 matrix defines for us a transformation of the plane. Suppose we are given two matrices A equals A_{1 1}, A_{2 2}; A_{2 1}, A_{2 2} and B equals B_{1 1}, B_{1 2}; B_{2 1}, B_{2 2}. They each define a transformation of the plane. What happens if we first do the transformation associated to B, and then do the transformation associated to A?
We get a new transformation associated to a new matrix, which we call A B. A times (B times v) equals A_{1 1}, A_{2 2}; A_{2 1}, A_{2 2} times (B_{1 1}, B_{1 2}; B_{2 1}, B_{2 2} times x, y) which equals A_{1 1}, A_{2 2}; A_{2 1}, A_{2 2} times the vector B_{1 1} x + B_{1 2} y, B_{2 1} x + B_{2 2} y, which equals A_{1 1} B_{1 1} x + A_{1 1} B_{1 2} y + A_{1 2} B_{2 1}x + A_{1 2} B_{2 2}y, A_{2 1} B_{1 1} x + A_{2 1} B_{1 2} y + A_{2 2} B_{2 1} x + A_{2 2} B_{2 2} y, which equals the matrix A_{1 1} B_{1 1} + A_{1 2} B_{2 1}, A_{1 1} B_{1 2} + A_{1 2} B_{2 2}; A_{2 1} B_{1 1} + A_{2 2} B_{2 1}, A_{2 1} B_{1 2} + A_{2 2} B_{2 2} times the vector x, y which we define to be the matrix A B times the vector v
Given matrices A equals A_{1 1}, A_{2 2}; A_{2 1}, A_{2 2}, and B equals B_{1 1}, B_{1 2}; B_{2 1}, B_{2 2}, we define the matrix product A times B to be the matrix A_{1 1} B_{1 1} + A_{1 2} B_{2 1}, A_{1 1} B_{1 2} + A_{1 2} B_{2 2}; A_{2 1} B_{1 1} + A_{2 2} B_{2 1}, A_{2 1} B_{1 2} + A_{2 2} B_{2 2}.
How on earth can we remember this formula? Here is a mnemonic. Just like when we act on a vector using a matrix, we can think of the entries of A B as "multiplying a row of A into a column of B". More specifically, to get the ijth entry of A B (i.e. ith row and jth column) we multiply the ith row of A into the jth column of B:
