a, b, c; d, e, f is a 2-by-3 matrix.
03. Bigger matrices
03. Bigger matrices
Bigger matrices
Just as a 2-by-2 matrix defines a transformation of the plane, an m-by-n matrix defines a transformation R n to R m. An m-by-n matrix is a rectangular array of numbers with m rows and n columns.
The transformation R n to R m associated to an m-by-n matrix M is the map v maps to M v where:
-
v is the vector x_1, x_2, dot dot dot, x_n,
-
M is the m-by-n matrix whose first row is M_{1 1}, M_{1 2}, dot dot dot, M_{1 n}, second row is M_{2 1}, M_{2 2}, dot dot dot, M_{2 n}, etc until the m-th row M_{m 1}, M_{m 2}, dot dot dot, M_{m n}.
-
M v is the vector whose jth entry is obtained by multiplying the jth row of M into the column vector v, that is M v equals M_{1 1}x_1 plus M_{1 2}x_2 plus dot dot dot plus M_{1 n} x_n, M_{2 1}x_1 plus M_{2 2}x_2 plus dot dot dot plus M_{2 n} x_n dot dot dot, M_{m 1}x_1 plus M_{m 2}x_2 plus dot dot dot plus M_{m n} x_n.
This vector M v has height m because there are m rows of M to multiply into the vector v.
For example, a, b, c; d, e, f; g, h, i times x, y, z equals a x plus b y plus cz, d x plus e y plus f z; g x plus h y plus iz shows how a 3-by-3 matrix eats a vector of height 3 and outputs a vector of height 3.
Take M to be the 3-by-3 matrix cos theta, minus sine theta, 0; sine theta, cos theta, 0; 0, 0, 1. We get M v equals x cos theta minus y sine theta, x sine theta plus y cos theta, z. We see that this is a rotation of 3-dimensional space which fixes the z-axis and rotates by theta in the x y-plane. We call it a rotation by theta about the z-axis.
Take M to be the 2-by-3 matrix 1, 0, 0; 0, 1, 0.. We need to feed M a vector of height 3; it will output a vector of height 2. In other words, M defines a transformation from R 3 to R 2. What is the transformation? 1, 0, 0; 0, 1, 0 times x, y, z equals x, y This is the projection to the x y-plane (which squishes the z-axis to the origin).
Take M to be the 3-by-2 matrix 1, 0; 0, 1; 0, 0. This gives a map from R 2 to R 3: 1, 0; 0, 1; 0, 0 times x, y equals x, y 0 This is the inclusion map of the 2-dimensional x y-plane into 3-dimensional space (putting it at height zero).
These rectangular (nonsquare) matrices change the dimension of the space we're working with, e.g. map from a lower to a higher dimensional space or vice versa. You might wonder why we matrices which are bigger than 3-by-3, given that we live in a 3-dimensional universe. In fact:
the theory of special relativity treats space and time on an equal footing, and the Lorentz transformations, which describe all the weird relativistic effects like time dilation and length contraction, mix up space and time, and are given by 4-by-4 matrices.
in statistics, data is often represented as a vector of samples; the more samples you have, the bigger the dimension of the vector you need to encode them.
More examples
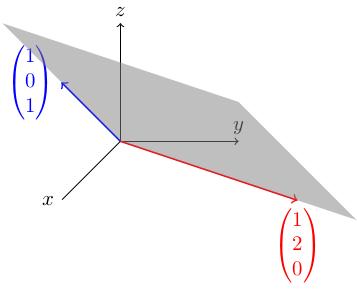
Take M to be the 3-by-2 matrix 1, 1; 2, 0; 0, 1. This defines a map from R 2 to R 3: M times x, y equals x plus y, 2 x, y. What does this map "look like"? Its image (the set of points in 3d which have the form M v for some v in R 2) is a plane. To visualise the plane, we and draw the images of the x- and y-axes in R 2:
-
The x-axis (vectors of the form x, 0) goes to the set of vectors x, 2 x, 0.
-
The y-axis (vectors of the form 0, y) goes to the set of vectors y, 0, y.
The image of M is the unique plane containing these two lines.
Take M to be the 2-by-3 matrix 1, 0, minus 1, 0, 1, minus 1. This defines a map from R 3 to R 2: 1, 0, minus 1; 0, 1, minus 1 times x, y, z equals x minus z, y minus z What does this map look like? Let's imagine it's projecting from 3-dimensional space onto the x y-plane (by including R 2 into R 3 as the x y-plane). The points x, y, 0 on the x y-plane go to x, y, 0 (i.e. they stay where they are). The point 0, 0, 1 on the z-axis goes to minus 1, minus 1. This means that everything is being projected onto the x y-plane; the projection is along straight line rays which point in the minus 1, minus 1, minus 1-direction (because to get from 0, 0, 1 to minus 1, minus 1, 0 you have to go backwards 1 in each of the x, y and z directions. This map is therefore a projection.
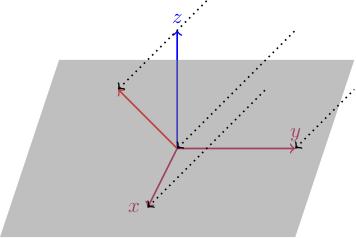
This line along which we're projecting has a name: it's called the kernel of M. More on this later.