36. Eigenapplications, 2: Ellipses

0.00 An ellipse is a curve in the plane: it looks like a squashed circle:

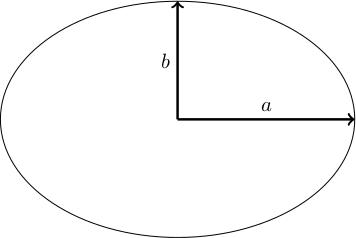
An ellipse with semimajor/minor axes a and b

The one in the diagram above has been squashed/stretched vertically/horizontally, and has equation $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ . Here, $a$ is the biggest value that $x$ can take (because if $x=a$ then $y$ has to be zero) and $b$ is the biggest value that $y$ can take. Suppose $a>b$ . If you look at diameters (chords of the ellipse passing through the origin) then the longest will have length $2a$ (pointing in the $x$ -direction) and the shortest will have length $2b$ (pointing vertically). We call $a$ the semimajor axis and $b$ the semiminor axis.

2.41 Suppose someone gives you an ellipse that has been squashed in some other direction. What is the equation for it? Conversely, if someone gives you the equation of an ellipse, how do you figure out the semimajor and semiminor axes?

General equation of an ellipse

3.10 What's the general equation of an ellipse? Assuming its centre of mass is at the origin, the general equation has the form $Ax^{2}+Bxy+Cy^{2}=1.$ If I wanted the centre of mass to be elsewhere, I could add terms like $Dx+Ey$ .

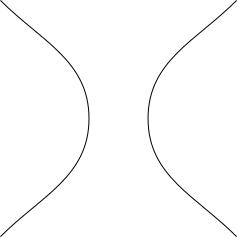
4.22 The constants $A, B, C$ can't be just anything. For example, if we take $A=1$ , $B=0$ , $C=-1$ , then we get $x^{2}-y^{2}=1$ , which is the equation of a hyperbola:

5.11 The condition on $A, B, C$ we need to get an ellipse is positive definiteness:

Definition:

The quadratic form $Ax^{2}+Bxy+Cy^{2}$ is positive definite if it's positive whenever we substitute in real numbers $x, y$ other than $0,0$ .

Definition:

6.19 An ellipse is a subset of $\mathbf{R}^{2}$ cut out by the equation $Ax^{2}+Bxy+Cy^{2}=1$ where $A, B, C$ are constants making the left-hand side positive definite.

Normal form for ellipses

Theorem:

7.08 Consider the matrix $M:=\begin{pmatrix}A&B/2\\ B/2&C\end{pmatrix}$ . Let $u_{1},u_{2}$ be unit length eigenvectors of $M$ (with eigenvalues $\lambda_{1},\lambda_{2}$ ). Pick coordinates so that the new $x$ - and $y$ -axes point along the eigenvectors $u_{1},u_{2}$ (and so that $u_{1}$ sits at $(1,0)$ and $u_{2}$ sits at $(0,1)$ ). In these new coordinates, the equation of the ellipse becomes $\lambda_{1}x^{2}+\lambda_{2}y^{2}=1.$

9.30 This change of coordinates will actually be a rotation of the usual coordinates.

9.46 The matrix $M$ arises as follows. Let $v=\begin{pmatrix}x\\ y\end{pmatrix}$ . Then $Ax^{2}+Bxy+Cy^{2}=v^{T}Mv.$

Lemma:

11.16 If $\lambda_{1}\neq\lambda_{2}$ then the eigenvectors $u_{1}$ and $u_{2}$ are orthogonal to one another. This works for any matrix $M$ for which $M^{T}=M$ .

12.14 We have $Mu_{1}=\lambda_{1}u_{1}$ and $Mu_{2}=\lambda_{2}u_{2}$ . Consider $u_{1}^{T}Mu_{2}$ . We have: $u_{1}^{T}Mu_{2}=u_{1}^{T}\lambda_{2}u_{2}$ $=\lambda_{2}u_{1}\cdot u_{2}.$ We also have $u_{1}^{T}Mu_{2}=u_{1}^{T}M^{T}u_{2}$ (because $M^{T}=M$ ), so $u_{1}^{T}Mu_{2}=u_{1}^{T}M^{T}u_{2}$ $=(Mu_{1})^{T}u_{2}$ $=\lambda_{1}u_{1}^{T}u_{2}$ $=\lambda_{1}u_{1}\cdot u_{2}.$ 13.46 Therefore $(\lambda_{1}-\lambda_{2})u_{1}\cdot u_{2}=0$ . Since $\lambda_{1}\neq\lambda_{2}$ , we can divide by $\lambda_{1}-\lambda_{2}$ and get $u_{1}\cdot u_{2}=0$ .

14.15 This is why the change of coordinates in the theorem is just a rotation: your eigenvectors are orthogonal, so just rotate your $x$ and $y$ -directions until they point in these directions.

Proof of theorem

14.35 In the new coordinates (which I'm still calling $x, y$ ), we have $v=xu_{1}+yu_{2}$ , so: $v^{T}Mv=(xu_{1}+yu_{2})^{T}M(xu_{1}+yu_{2})$ $=(xu_{1}+yu_{2})^{T}(x\lambda_{1}u_{1}+y\lambda_{2}u_{2})$ $=x^{2}\lambda_{1}+y^{2}\lambda_{2},$ where we have used $u_{1}\cdot u_{1}=u_{2}\cdot u_{2}=1$ and $u_{1}\cdot u_{2}=0$ . This proves the theorem.

Semimajor and semiminor axes

17.17 The theorem tells us that the semimajor and semiminor axes point along the eigenvectors of $M$ . Comparing the equations, we see that the semimajor and semiminor axes are $a=\frac{1}{\sqrt{\lambda_{1}}}$ and $b=\frac{1}{\sqrt{\lambda_{2}}}$ .

Example

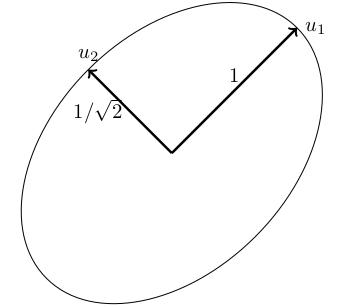
18.36 Consider the ellipse $\frac{3}{2}(x^{2}+y^{2})-xy=1.$ The matrix $M$ is $M=\begin{pmatrix}\frac{3}{2}&-\frac{1}{2}\\ -\frac{1}{2}&\frac{3}{2}\end{pmatrix}.$ 19.17 This has characteristic polynomial $\det\begin{pmatrix}3/2-t&-1/2\\ -1/2&3/2-t\end{pmatrix}=t^{2}-3t+2$ , which has roots $\frac{3\pm\sqrt{9-8}}{2}$ , i.e. $\lambda_{1}=1$ and $\lambda_{2}=2$ .

20.27 The unit eigenvectors are:

for $\lambda_{1}=1$ , $u_{1}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ 1\end{pmatrix}$ ,
for $\lambda_{2}=2$ , $u_{2}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ -1\end{pmatrix}$ .

21.57 What does this tell us? The semimajor and semiminor axes point in the $u_{1}$ - and $u_{2}$ -directions: rotated by $45$ degrees from the usual axes. The lengths are $a=\frac{1}{\sqrt{\lambda_{1}}}=1$ and $b=\frac{1}{\sqrt{\lambda_{2}}}=\frac{1}{\sqrt{2}}$ .

An ellipse with semimajor and minor axes 1 and 1/\sqrt{2}, with semimajor axis pointing in the (1,1)-direction

Ellipsoids

24.07 Exactly the same thing works in higher dimensions: an ellipsoid is given by $Q(x_{1},\ldots,x_{n})=1$ where $Q$ is a positive definite quadratic form, $Q(v)=v^{T}Mv$ for some symmetric matrix $M$ , and the ellipsoid is related to the standard ellipsoid $\sum\frac{x_{k}^{2}}{a_{k}^{2}}=1$ by rotating so that the $x_{1},\ldots,x_{n}$ axes point along the eigendirections of $M$ . The coefficients $a_{k}$ are given by $\frac{1}{\sqrt{\lambda_{k}}}$ where $\lambda_{k}$ are the eigenvalues.