The quadratic form A x squared + B x y + C y squared is positive definite if it's positive whenever we substitute in real numbers x, y other than 0, 0.
36. Eigenapplications, 2: Ellipses
36. Eigenapplications, 2: Ellipses
An ellipse is a curve in the plane: it looks like a squashed circle:
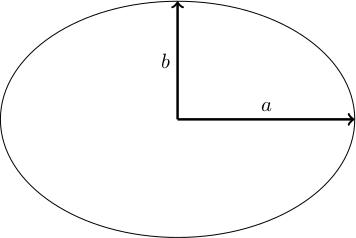
The one in the diagram above has been squashed/stretched vertically/horizontally, and has equation x squared over a squared + y squared over b squared = 1. Here, a is the biggest value that x can take (because if x = a then y has to be zero) and b is the biggest value that y can take. Suppose a is bigger than b. If you look at diameters (chords of the ellipse passing through the origin) then the longest will have length 2 a (pointing in the x-direction) and the shortest will have length 2 b (pointing vertically). We call a the semimajor axis and b the semiminor axis.
Suppose someone gives you an ellipse that has been squashed in some other direction. What is the equation for it? Conversely, if someone gives you the equation of an ellipse, how do you figure out the semimajor and semiminor axes?
General equation of an ellipse
What's the general equation of an ellipse? Assuming its centre of mass is at the origin, the general equation has the form A x squared + B x y + C y squared = 1 If I wanted the centre of mass to be elsewhere, I could add terms like D x + E y.
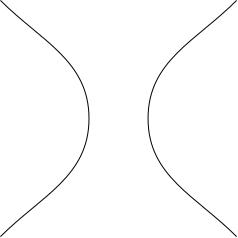
The constants A, B, C can't be just anything. For example, if we take A = 1, B = 0, C = minus 1, then we get x squared minus y squared = 1, which is the equation of a hyperbola:
The condition on A, B, C we need to get an ellipse is positive definiteness:
An ellipse is a subset of R^2 cut out by the equation A x squared + B x y + C y squared = 1 where A, B, C are constants making the left-hand side positive definite.
Normal form for ellipses
Consider the matrix M = A, B over 2; B over 2, C. Let u_1, u_2 be unit length eigenvectors of M (with eigenvalues lambda_1, lambda_2). Pick coordinates so that the new x- and y-axes point along the eigenvectors u_1, u_2 (and so that u_1 sits at (1, 0) and u_2 sits at (0, 1)). In these new coordinates, the equation of the ellipse becomes lambda_1 x squared + lambda_2 y squared = 1
This change of coordinates will actually be a rotation of the usual coordinates.
The matrix M arises as follows. Let v = x, y. Then A x squared + B x y + C y squared = v transpose M v
If lambda_1 is not equal to lambda_2 then the eigenvectors u_1 and u_2 are orthogonal to one another. This works for any matrix M for which M transpose = M.
We have M u_1 = lambda_1 u_1 and M u_2 = lambda_2 u_2. Consider u_1 transpose M u_2. We have: u_1 transpose M u_2 = u_1 transpose lambda_2 u_2, which equals lambda_2 u_1 dot u_2. We also have u_1 transpose M u_2 = u_1 transpose M transpose u_2 (because M tranpose = M), so u_1 transpose M u_2 = u_1 transpose M transpose u_2, equals M u_1 all transpose times u_2, which equals lambda_1 u_1 transpose u_2, which equals lambda_1 u_1 dot u_2. Therefore (lambda_1 minus lambda_2) all times u_1 dot u_2 equals 0. Since lambda_1 is not equal to lambda_2, we can divide by lambda_1 minus lambda_2 and get u_1 dot u_2 = 0.
This is why the change of coordinates in the theorem is just a rotation: your eigenvectors are orthogonal, so just rotate your x and y-directions until they point in these directions.
Proof of theorem
In the new coordinates (which I'm still calling x, y), we have v = x u_1 + y u_2, so: v transpose M v = (x u_1 + y u_2) transpose M times (x u_1 + y u_2), which equals (x u_1 + y u_2) transpose times (x lambda_1 u_1 + y lambda_2 u_2), which equals x squared lambda_1 + y squared lambda_2 where we have used u_1 dot u_1 = u_2 dot u_2 =1 and u_1 dot u_2 = 0. This proves the theorem.
Semimajor and semiminor axes
The theorem tells us that the semimajor and semiminor axes point along the eigenvectors of M. Comparing the equations, we see that the semimajor and semiminor axes are a = 1 over root lambda_1 and b = one over root lambda_2.
Example
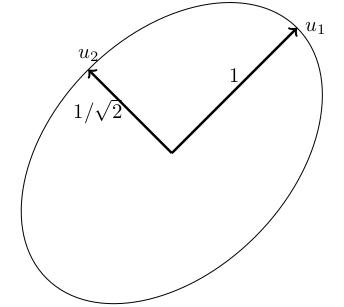
Consider the ellipse 3 over 2 times (x squared plus y squared), minus x y = 1 The matrix M is M = 3 over 2, minus 1 over 2; minus 1 over 2, 3 over 2. This has characteristic polynomial det of 3 over 2 minus t, minus a half, minus a half, 3 over 2 minus t, which equals t squared minus 3 t + 2, which has roots 3 plus or minus root 9 minus 8, all over 2, i.e. lambda_1 = 1 and lambda_2 = 2.
The unit eigenvectors are:
-
for lambda_1 = 1, u_1 = 1 over root 2 times the vector 1, 1,
-
for lambda_2 = 2, u_2 = 1 over root 2 times the vector 1, minus 1.
What does this tell us? The semimajor and semiminor axes point in the u_1- and u_2-directions: rotated by 45 degrees from the usual axes. The lengths are a = 1 over root lambda_1 = 1 and b = 1 over root lambda_2 = 1 over root 2.
Ellipsoids
Exactly the same thing works in higher dimensions: an ellipsoid is given by Q of x_1 up to x_n = 1 where Q is a positive definite quadratic form, Q of v equals v transpose M v for some symmetric matrix M, and the ellipsoid is related to the standard ellipsoid sum of x_k squared over a_k squared = 1 by rotating so that the x_1 up to x_n axes point along the eigendirections of M. The coefficients a_k are given by 1 over root lambda_k where lambda_k are the eigenvalues.