We have the limit as n goes to infinity of F_{n + 1} over F_n = 1 + root 5, all over 2. This expression is the "golden ratio" 1 point 6 1 8 dot dot dot.
37. Eigenapplications, 3: Dynamics
37. Eigenapplications, 3: Dynamics
We now turn to dynamics. Let v be a vector and A be a matrix. Consider the sequence v, A v, A squared v, A cubed c, etc. We'll investigate what happens to this sequence A to the n v as n goes to infinity.
Example: Fibonacci sequence
Let A = 0, 1; 1, 1 and v = 1, 1. We get A v = 1, 2; A squared v = 2, 3; A cubed v = 3, 5; to the 4 v = 5, 8, and, more generally, A to the n v = F_n, F_{n+1} where F_0 = 1, F_1 = 1, F_2 = 2, F_3 = 3, F_4 = 5, F_5 = 8, F_6 = 13 is the Fibonacci sequence.
Why are we getting the Fibonacci numbers? Suppose the formula A to the n v = F_n, F_{n+1} is true for some value of n; we'll prove it's true for all values of n by induction: A to the n + 1 v = A A to the n v = A times F_n, F_{n+1}, which equals F_{n+1}, F_n + F_{n+1}, which equals F_{n+1}, F_{n+2} where we used the recursive formula F_{n + 2} = F_{n + 1} + F_n which defines the Fibonacci sequence.
As n goes to infinity, both entries of the vector tends to infinity, but they do so in a particular way:
Write v = 1, 1 as alpha u_1 + beta u_2 where u_1 and u_2 are the lambda_1- and lambda_2-eigenvectors of A = 0, 1; 1, 1. We'll figure out what these eigenvectors and eigenvalues are later.
Now A to the n v = A to the n times (alpha u_1 + beta u_2), which equals alpha A to the n u_1 + beta A to the n u_2. We have A u_1 = lambda_1 u_1, A squared u_1 = lambda_1 A u_1 = lambda_1^2 u_1, and by induction we get A to the n u_1 = lambda_1 to the n u_1 and A to the n u_2 = lambda_2 to the n u_2. Therefore F_n, F_{n + 1} = A to the n v = alpha lambda_1 to the n u_1 + beta lambda_2 to the n u_2.
I claim that lambda_1 = (1 + root 5) all over 2, which is approximately 1 point 6 1 8 dot dot dot and lambda_2 = (1 minus root 5), all over 2, which is approximately minus 0 point 6 1 8 dot dot dot. Therefore:
-
lambda_1 is strictly bigger than 1, so lambda_1 to the n tends to infinity,
-
lambda_2 to the n tends to 0 as n tends to infinity. Note that lambda_2 is negative, so its powers keep switching sign, but its absolute value is less than 1, so the absolute value of its powers get smaller and smaller as n goes to infinity.
Therefore the limit as n goes to infinity of F_{n + 1} over F_n is the limit of the slopes of the vectors alpha lambda_1 to the n u_1 + beta lambda_2 to the n u_2, and the lambda_2 to the n term is going to zero, so in the limit we just get the slope of the vector alpha lambda_1 to the n u_1, which is just a rescaling of u_1. Since rescaling doesn't change the slope, we get the limit as n goes to infinity of F_{n + 1} over F_n equals the slope of u_1
We therefore need to figure out the slope of u_1 (and verify the claim about eigenvalues). The characteristic polynomial of A is det of minus t, 1; 1, 1 minus t, which equals t squared minus t + 1, whose roots are 1 plus or minus root 5, all over 2 as required. The eigenvectors are 1, 1 plus or minus root 5 all over 2, so u_1 (corresponding to the plus sign) has slope 1 + root 5, all over 2, as required.
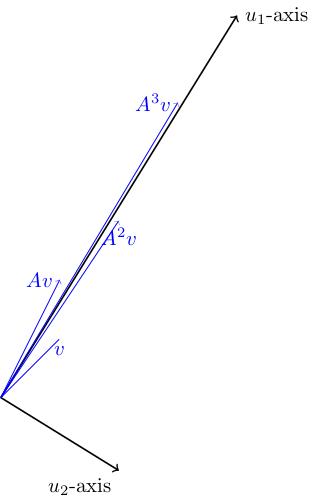
Here's a picture of the eigenlines (orthogonal to one another because the matrix A is symmetric) and the positions of v, A v, A squared v, etc. You can see that these vectors get closer and closer to the u_1-eigenline (and stretched out in the u_1-direction). They move from side to side of this axis because the sign of lambda_2 is negative. So A to the n v gets more and more parallel to u_1 as n goes to infinity.
Arnold cat map
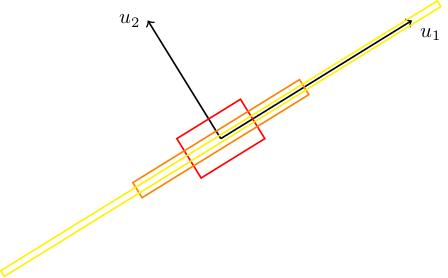
Here's another nice example, due to Vladimir Arnold. Consider A = 2, 1; 1, 1. This has eigenvalues 3 plus or minus root 5, all over 2: one of these is bigger than 1, the other is positive but less than 1. Here are the eigenlines, with a square S drawn on (whose sides are parallel to the eigenlines). We also draw A(S) and A squared (S). We can see that it gets stretched in the u_1-direction and squashed in the u_2-direction (because lambda_1 is strictly bigger than 1 and lambda_2 is strictly less than 1). In the limit, A to the n (S) gets thinner and thinner and closer to the u_1-eigenline.
This is called the Arnold cat map because of the following strange phenomenon. Take an infinite grid of squares in R^2, take a picture of a cat, and put it into every square. Apply A to this grid of cats. The cats will get stretched and squashed in the eigendirections. Pick one of our original squares and look at what's there. We see a bunch of cats all chopped up and stretched and squished back into that square in some way. Now repeat, and repeat. What we see in our square is absolute carnage for a long time. But, amazingly, at some point, we our cat reappears almost identically to how it looked to begin with. This is not because of any periodicity: A to the n is not the identity for any positive n. This is instead an instance of "Poincaré recurrence": a phenomenon in dynamical systems which goes way beyond anything we're discussing in this course.